Earthquake Response Spectra[地震反应谱]

•  反应谱的基本概念（Introduction to Response Spectra）

地震动反应谱：单自由度弹性系统对于某个实际地震加速度的最大反应（可以是加速度、速度和位移）和体系的自振特征（自振周期或频率和阻尼比）之间的函数关系。工程中常用到反应谱的概念，如，我们目前采用的是基于反应谱的抗震设计方法、在静力弹塑性分析的时候我们还需要用到反应谱、在动力时程分析选择地震波的时候，我们还常需要以规范的设计反应谱为参考，要求选择的地震波的反应谱和设计反应谱相比不能偏差过大。

• 反应谱的理论公式（Basic Equations of Response Spectra） 

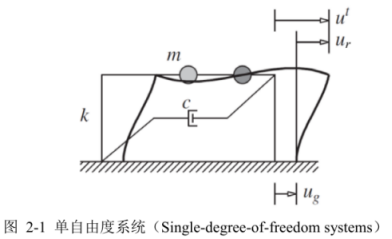
单自由度地震作用下的动力方程：

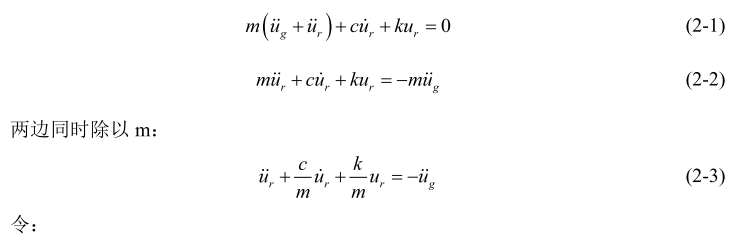
从公式(2-5)可知，结构的地震动响应只和 3 个变量有关：地面加速度（）、结构的阻尼比（ξ）和无阻尼结构体系的圆频率（ω）。因此对于一个给定的地震动，结构的位移响应u_r 是圆频率（ω）和阻尼比（ξ）的函数。根据反应谱的概念，对于特定的地震波，只要选定阻尼比ξ，结构的最大响应（包括，速度、位移和加速度）是结构频率ω的函数，对一条特定的地震波，圆频率（ω）取不同的值进行动力时程分析，将获得响应最大值作为纵坐标，圆频率（ω）为横坐标绘图，就得到反应谱曲线。

• 常用的地震反应谱（Commonly used Response Spectra）

（1）反应谱（Response Spectra）

当最大响应分别取相对位移、相对速度、绝对加速度时，我们可获得以下反应谱：

相对位移反应谱：

相对速度反应谱：

绝对加速度反应谱：

（2）伪反应谱（Pseudo-Response Spectra）

另外，工程中还常用到伪反应谱。所谓伪反应谱是指，当我们获得相对位移位移反应谱后，通过以下公式获得伪相对速度反应谱、伪绝对加速度反应谱：

伪相对速度反应谱：

伪绝对加速度反应谱：

事实上，在基于强度的设计方法里，常用的是伪绝对加速度反应谱 PSA (ξ ω)，而不是绝对加速度反应谱 SA (ξ ω)。原因是，我们基于反应谱的设计方法实际上是一种等效静力设计方法。所谓等效静力法的意思是，结构在地震作用下是一个动力过程，但是动力方程太复杂，还是希望采用一种静力的思维方式（ F=ku ）来设计结构，只要保证设计出来的结构其变形（ F /k ）与结构在真实地震动作用下的变形u_r 相等就可以了。

以单自由度为例进行说明，如下公式是单自由度的地震加速度作用下的动力方程：

将以上公式移项可得：

假设上式中结构的位移响应u_r为真实地震动作用下的值，则ku_r对应一个等效静力，其左边除了绝对加速度产生的惯性力 外，还有一个阻尼项。

如果我们的设计反应谱为绝对加速度反应谱，也就是说采用（即设计内力取结构的真实惯性力），那么在给定 k （设计时候给定截面尺寸、从而确定构件的刚度）的情况下，按内力 设计的构件，其在真实地震动作用下的变形和按静力思维获得的变形不相同。或者换句话来说，按 设计的结构，其是否能承受预期的地震动是不准确的。回想我们做结构设计的时候，我们确实都采用反应谱法计算力，并直接用计算出来的力进行配筋了，并没有考虑到阻尼项对力进行修正。

那么，问题出在哪？设计内力不取，那么应该取什么。我们可以反过来思考，为了保证设计出来的结构其变形（ F/ k ）与结构在真实地震动作用下的变形u_r相等，则设计内力必须为F=ku_r 。对于单自由度体系，由公式(2-4)可知， k=mω²= 。则设计内力应该为 F=mω²u_r。由于动力时程结果有很多点，设计时我们关心的是最大响应，则有：

由伪加速度反应谱的公式可以得：

从公式(3-2)可知，只要我们采用伪加速度反应谱，以F =mPSA(ξ ,ω)为设计内力，那么设计出来的结构就可以承受该地震。因此，一般情况，规范的设计反应谱是绝对加速度反应谱，而且应该是基于伪绝对加速度反应谱建立。

对于多自由体系，其基本概念也是一样的，只不过是多了振型分解与组合的过程。

同时我们必须注意，上述阐述都是以结构相对位移u_r 为基础考虑的。如果我们比较关心的是真实的绝对加速度或者相对速度，那么在使用规范反应谱的时候就要注意。

（3）反应谱和伪反应谱的关系（Relation between Response Spectra and Pseudo-Response Spectra）

任意荷载作用下单自由度的响应可以用杜哈梅积分（Duhamel’s integral）来计算：

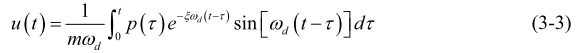
将荷载p(τ) 替换，u(t) 替换为u_r (t)将可得地震作用下单自由度体系的位移响应：

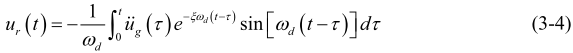
则位移反应谱和加速度反应谱分别为：

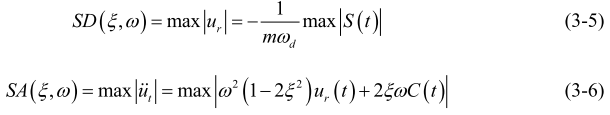其中：

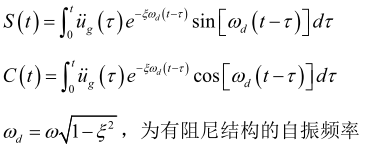
从公式（3-6）可以知，当阻尼比ξ=0时，，伪反应谱和反应谱相等。当考虑阻尼的时候，阻尼越大，伪反应谱和反应谱相差越大。

• 反应谱的数值计算方法与程序（Numerical methods and Program for Response Spectra）

有了上面的概念之后，我们就可以计算反应谱了。对于一般的加速度时程，常采用数值计算方法计算反应谱。数值计算方法又分为多种，有频域的有时域的。常用的时域计算方法有：精确逐步积分算法、常加速度法、线性加速度法、中心差分法、Newmark 法等。 目前常用的地震波反应谱计算软件有 SeismoSignal，该软件可以利用教育邮箱免费申请使用。利用数值计算方法，我们也可以自己编制地震波反应谱计算程序。

本文，编制了地震反应谱分析程序—SPECTR，用于批量计算反应谱，程序界面如下：

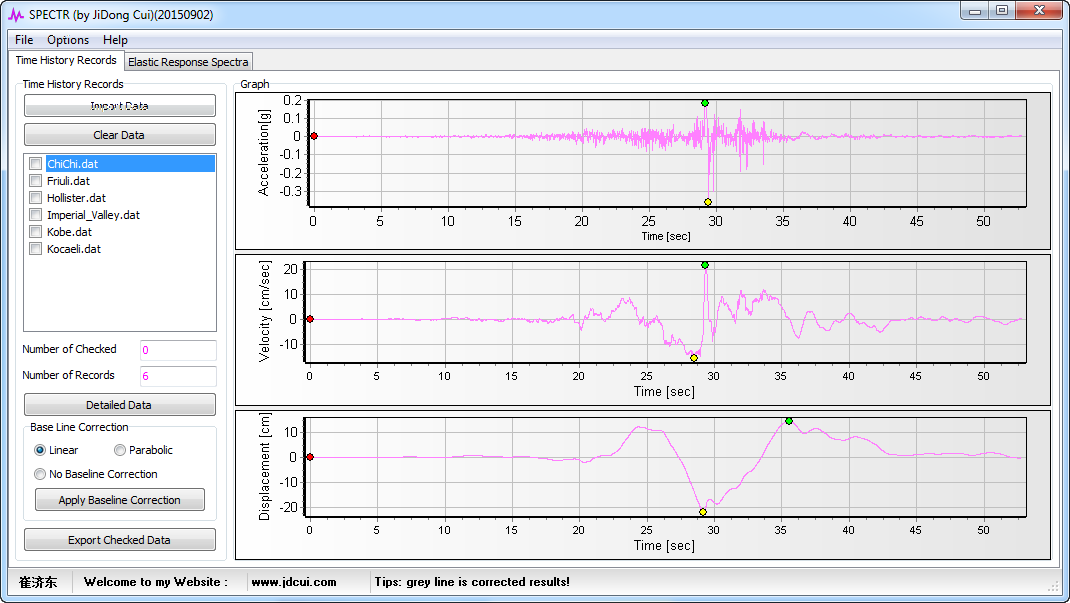
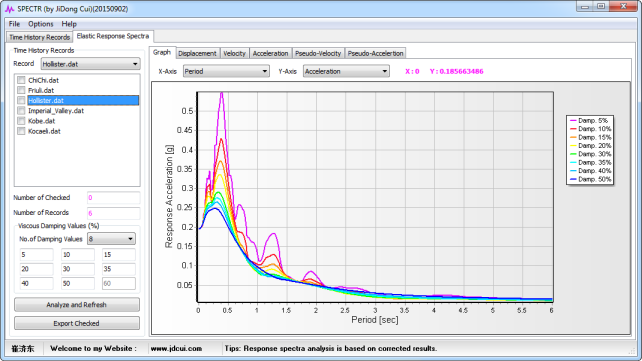
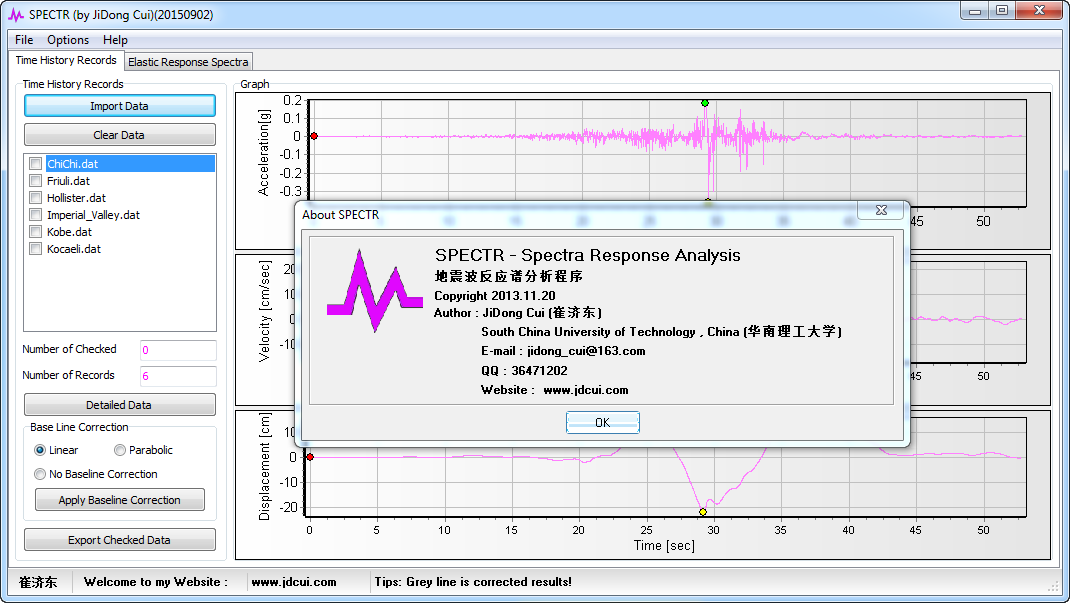
SPECTR 除了提供反应谱计算外，还可以对加速度时程进行基线修正和积分。

关于SPECTR的更多信息将会在接下来的博文中进行介绍。

SPECTR是免费的，可以在我的网站：www.jdcui.com 进行下载。

• 小结（Conclusions）

总结了地震反应谱的基本概念、基本公式、对反应谱和伪反应谱的概念进行了阐述，并编制了地震反应谱计算软件 SPECTR。如有错误或遗漏，欢迎大家批评指正。

• 参考文献（References）

[1] Chopra AK. Dynamics of Structures: Theory and Applications to Earthquake Engineering. Prentice-Hall: New Jersey, 2012.
[2] Clough RW, Penzien J. Dynamics of Structures. McGraw-Hill: New York, 1993

• 注释（Comments）

如有错误或者遗漏欢迎大家给我指出。有任何意见和建议，也欢迎大家联系我，我的邮箱：jidong_cui@163.com 。

• 微信公众号 ( Wechat Subscription)

欢迎关注 “结构之旅” 微信公众号