稳态热传导的控制方程与经典扭转理论的控制方程具有相似性。我们可以通过比拟,在通用有限元软件中利用稳态热传导分析的功能进行扭转问题的分析。本文结合ANSYS软件,通过一个实例说明这个比拟的具体过程。(The steady heat conduction problem and the classic torsion theory have analogy in their control partial differential equations. We can conduct a torsional analysis making use of the steady analysis fuction in general finite element program. This post gives an example on how to do torsion analysis as thermal analogy with ANSYS.)
- 稳态热传导控制方程与扭转控制方程 ( Control partial differential equations of steady heat conduction problem and classic torsion theory)
(1)稳态热传导控制方程
2D情况下的稳态热传导控制方程
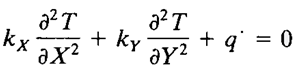
(2)St. Venant 扭转偏微分方程
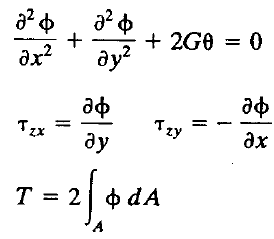
两者的偏微分方程均为Helmholtz方程的特殊形式。因此可以利用通用有限元软件中的稳态热传导分析功能通过比拟进行截面的扭转应力分析。
- 算例(Example)

- 有限元模拟(FEM Analysis)
利用ANSYS APDL进行分析,具体步骤如下:
(1)在前处理模块中新建单元类型(Create Element Type in Preprocessor Module)
采用77号单元
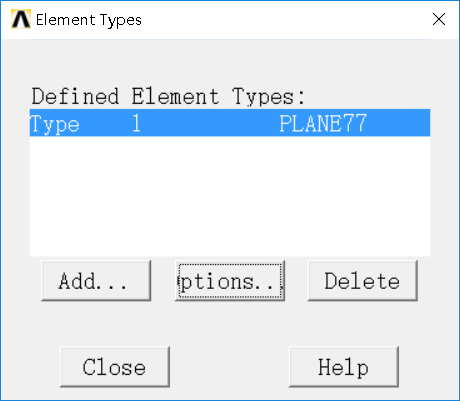
(2)在前处理模块中新建材料(Create Material in Preprocessor Module)
材料主要定义热传导系数
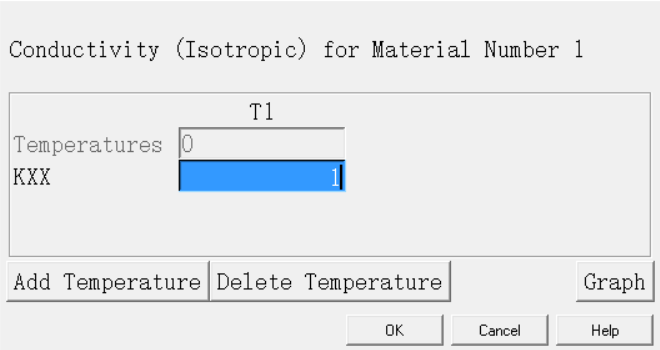
(3)在前处理模块创建面并划分网格(Create Area and Mesh in Preprocessor Module)

(4)施加零温度边界条件(Apply Zero Temperature Boundary Condition)
(5)施加热源(Apply Heat on Area)
等效热源:2Gθ = 2*76923*0.0005 = 76.923
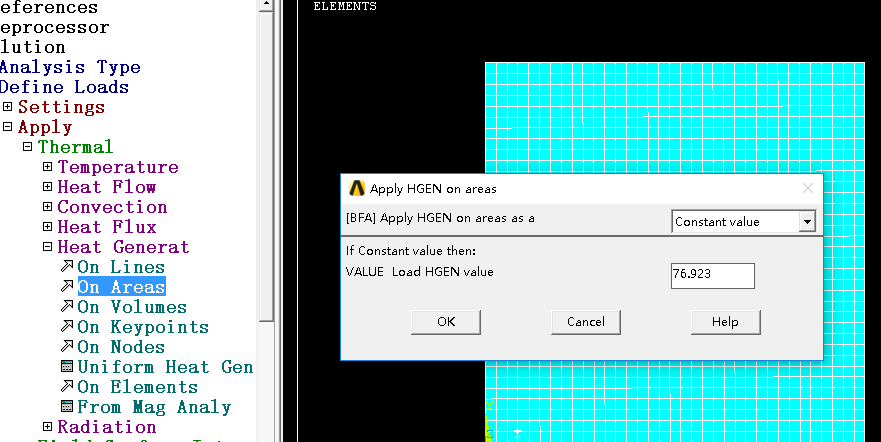
(6)求解有限元模型(Solve FEM model in Solution Module)
进行稳态热传导分析
(7)查看结果(Check Results)
- 查看分析结果(Results)
(1)查看节点温度 (Nodal Temperature)
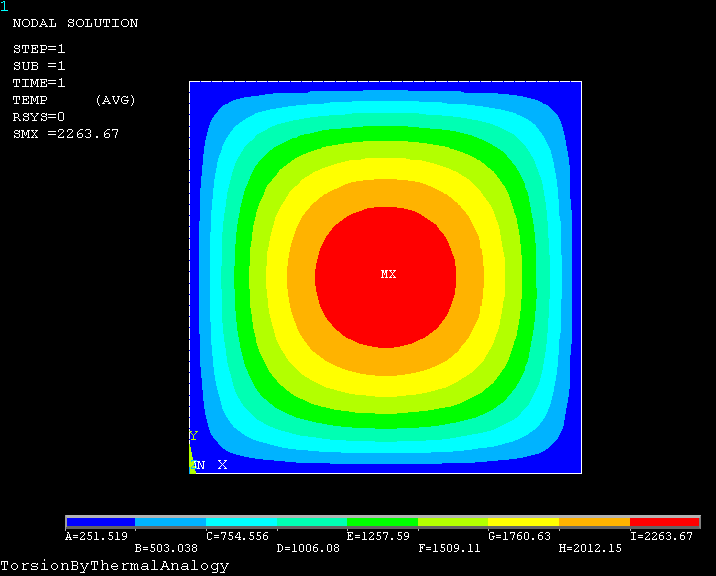
可以看出扭转应力函数的形状。
(2)查看温度梯度 (Nodal Temperature Gradient)
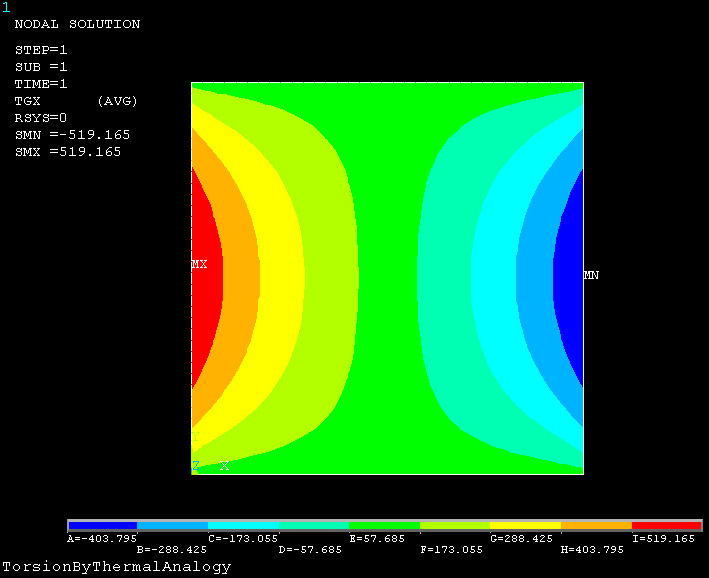
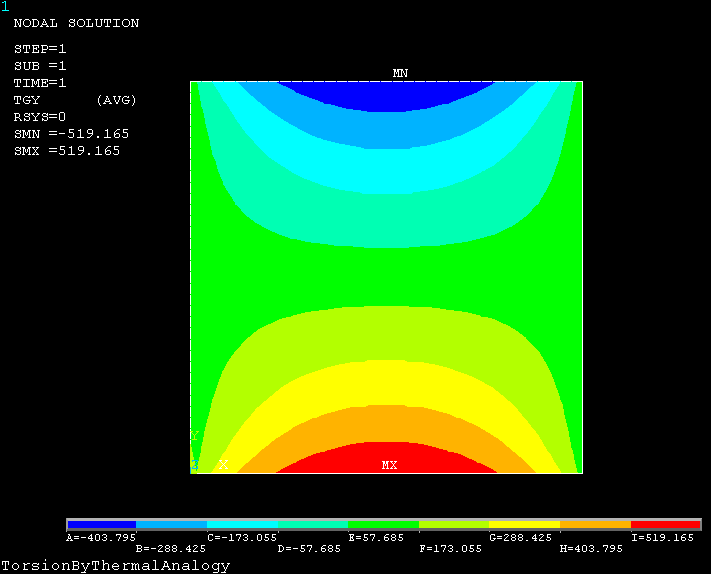
(3)查看热流量向量 (Thermal Flux Vector)
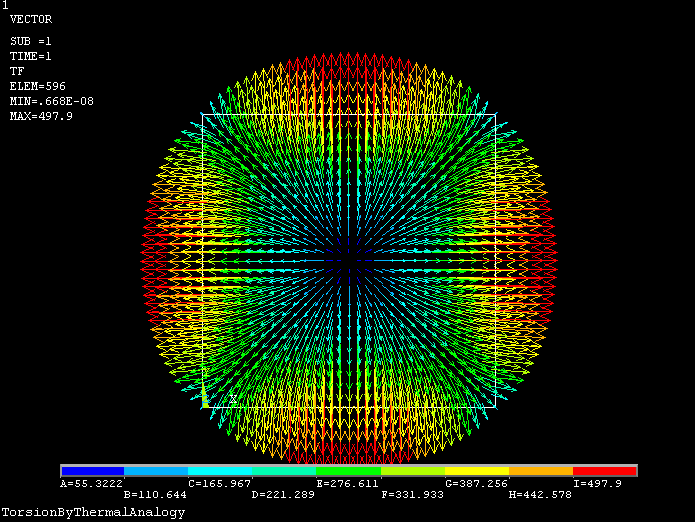
从热流量向量图也可以看出,矩形截面扭转剪切应力的分布:边的中间最大,角点为0。
- 与理论结果对比(Comparison with Theory )
根据弹性理论,θ = T/ (ab3Gβ1) , τmax = T/ (ab2β).
τmax = θ(ab3Gβ1) / (ab2β) = θbGβ1 / β = 0.0005*20*76923*0.141/0.208 = 521.4492Mpa
与分析结果 519.165Mpa相近。
- 注释 ( Comments )
( 大家一起学习有限元!!!! 如有错漏,欢迎批评指正。邮箱:jidong_cui@163.com . 如果你喜欢这篇博文,请在上面给我 点个赞 吧! 

( If you have found any problem about this post, please don’t hesitate to contact me directly.Email : jidong_cui@163.com. If you like this posts, please give me a “thumbs up“ rating on the above button! )
- 微信公众号 ( Wechat Subscription)
欢迎关注 “结构之旅” 微信公众号

