复习有限元知识，利用 Abaqus 进行欧拉-伯努利梁单元的分析。欧拉伯-努利梁理论（Euler–Bernoulli beam）又称为工程梁理论（Engineering beam theory）或者经典梁理论（Classical beam theory）。欧拉梁不考虑剪切变形，与铁木辛柯梁（Timoshenko beam）相对。Abaqus中的B23和B33单元为欧拉梁单元。
- 算例（Example）
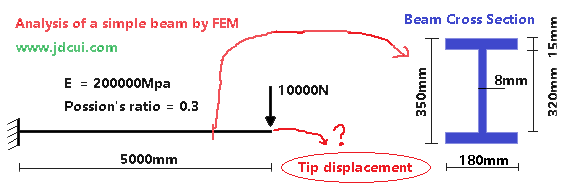
- 有限元模拟（FEM Analysis）
采用Abaqus进行分析，单元B23。基本步骤如下：
（1）设置工作路径并创建数据库（Set Work Directory and Create Model Database）
（2）创建部件（Create Part）
由于分析问题为2D，模型空间选为 2D Planar；类型为 Deformable；基本特性为 Wrie。（As the problem is 2D, set 2D Planar as the Modeling Space, Deformable as the Type and Wire as the Base Feature.）
使用点连接线命令绘制梁的几何特性（Use the Created-Lines Connected Command to draw the geometry of the beam）。
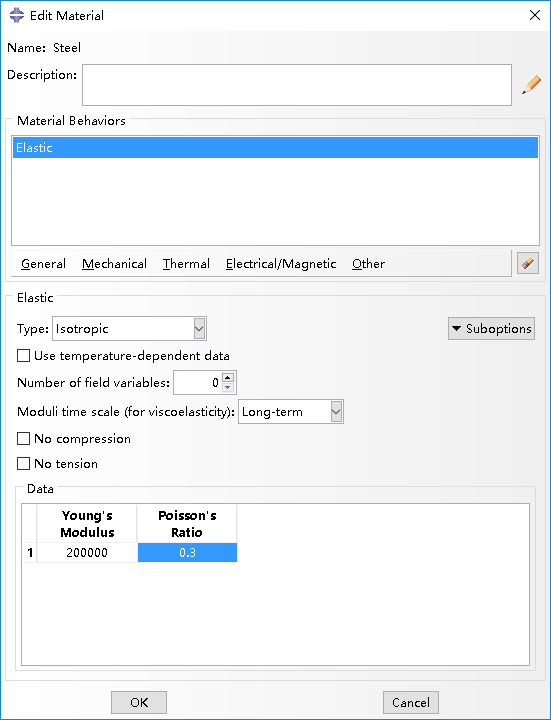
（3）创建材料 （Create Material）
在属性模块下（ Property）定义弹性材料，输入弹性模量和泊松比。Under the Property, create a elastic material and enter 200000 for Elastic Modulus and 0.3 for Possion’s Ratio.）
（4）创建梁截面轮廓（ Create Beam Profile）
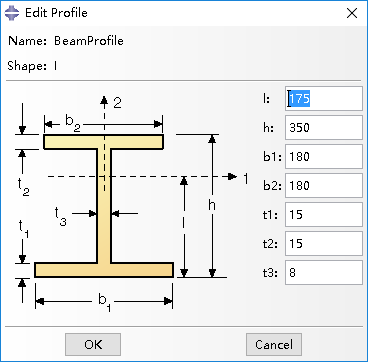
（5）创建截面 （Create Section）
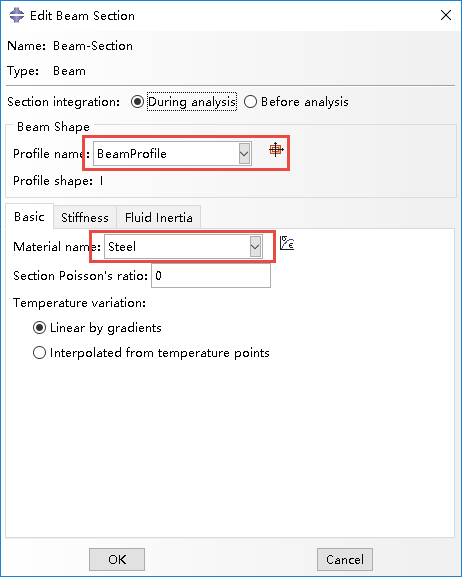（6）赋予截面 （Assign Section）
（7）赋予梁单元方向 （Assign Beam Orientation）
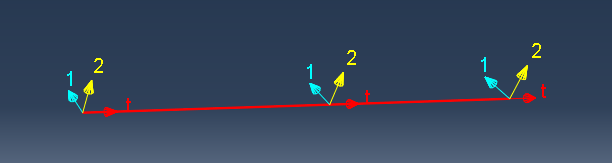
可以渲染梁的3D形状检查截面定义是否正确（Render the Beam Profile to Check the Orientation）
（8）划分部件网格 （Mesh Part）
赋予单元类型（Assign Element Type），如图选择B23，为欧拉梁单元。（Assign Element Type, Select the Linear for the Geometric Order, and Cubic formulation for the Beam type.）
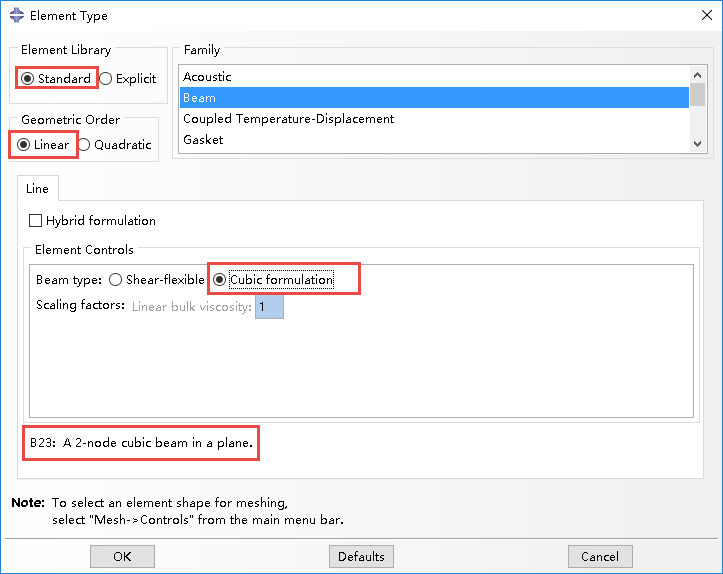
网格划分，本例只划分一个单元。
（9）在组装模块中创建实例，属性选择Parts（Create instance from Parts in Assembly Module）。
（10）定义荷载步（Create Load Step）
定义静力分析用的荷载步，类型为Static，General，不考几何非线性。（Defined a new step for static analysis.）
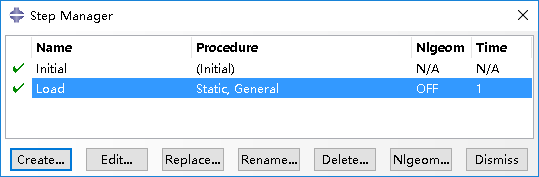
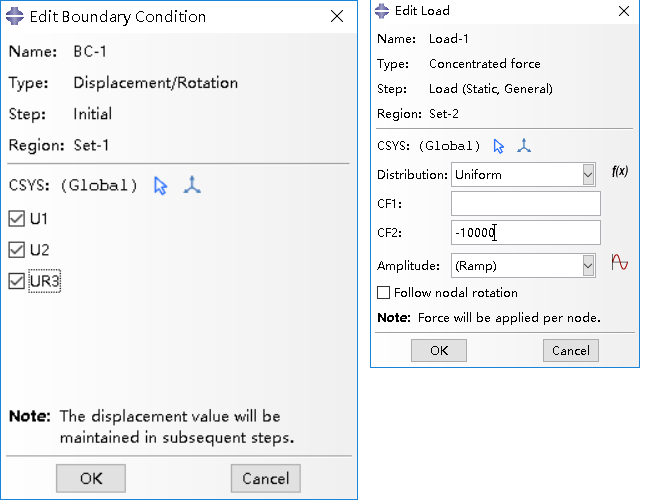
（11）定义荷载和约束 （Define load and constraint）
施加固端支座约束，施加节点力10000 。
（12）定义任务并运行分析 （Define Job and Submit to Run Analysis ）
（13）查看结果（Check Results）
- 结果分析（Results）
可在Visualization模块打开分析完的.odb文件查看分析结果。
（1）变形结果
（2）应力结果
（3）支座反力
- 与理论结果对比（Comparison with Theory ）
截面饶1轴的惯性矩 I=173450333.333333
端部位移的理论值 U2 = F*L3/3EI = 10000*50003/(3*200000*173450333.333333) = 12.0111 mm.
Abaqus 的分析结果
U.U2 = -12.0284，与理论结果相近。造成这种差别主要是Abaqus内部计算的惯性矩的值与理论值可能有差异。
- 注释 ( Comments )
( 如有错漏，欢迎批评指正。Email : jidong_cui@163.com)
( If you have found any problem about this post, please don’t hesitate to contact me directly. Email : jidong_cui@163.com)
- 微信公众号 ( Wechat Subscription)
欢迎关注 “结构之旅” 微信公众号
