康威常数 (Conway’s Constant) 是 Look-and-say sequence 相邻两项数字长度的比值的极限,常用希腊字母λ表示,约等于1.303577,由数学家 John Conway 发现。
Look-and-say sequence 序列的前10行:
1: 11
2: 21
3: 1211
4: 111221
5: 312211
6: 13112221
7: 1113213211
8: 31131211131221
9: 13211311123113112211
10: 11131221133112132113212221
第n项是对第n-1项的描述。随着n的不断增加,第n+1项的长度和第n项的长度的比值趋向于1.3,极限值为1.303577,这个数就是康威常数。
用程序测试一下 😎 。
思路:
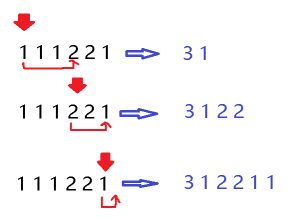
测试:
2项,比值为2。
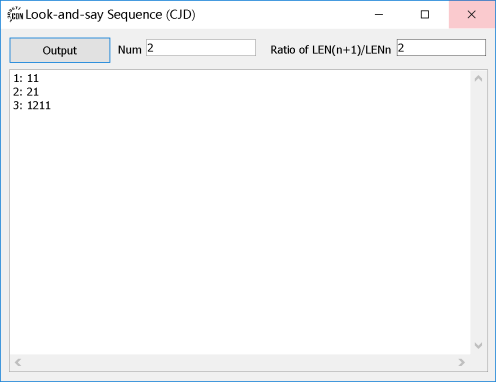
5项,比值为1.3333333333333333。
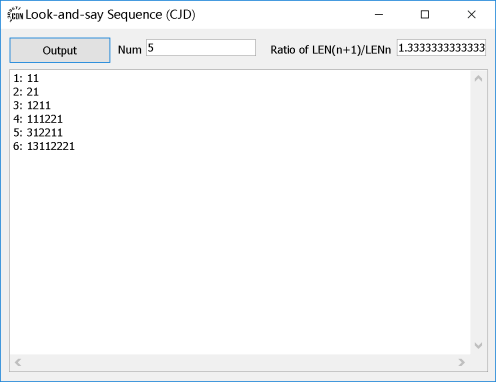
10项,比值为1.30769230769231。
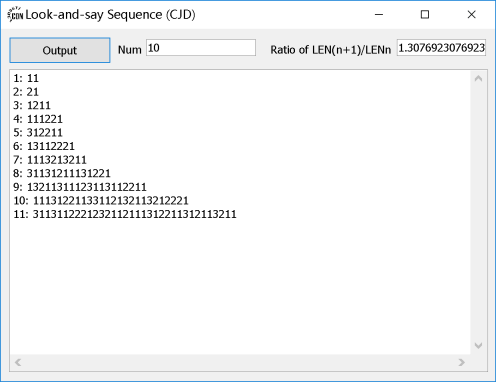
50项,比值为1.30372985028826。
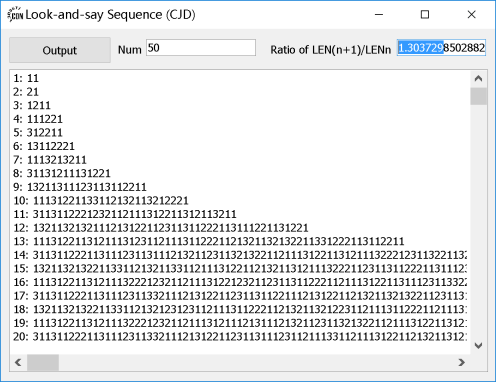
可见比值越来越接近1.303577,即长度增长按30%的速度增加。
无所不在的数学!!! 😀 😀 😀
