实干、实践、积累、思考、创新。
拍振现象指的是两个频率接近的力（激励源）产生的振动叠加在一起，由于频率接近，周期也接近，每过一个周期两个信号的相对相位就会有一点变化，接近同相的时候两个信号叠加，幅值变大；接近反相的时候两个信号相互抵消，幅值变小，造成波形总幅值的周期性波动。
这里有一些不错的介绍资料，一并列出：
[1] Beats：https://www.physicsbootcamp.org/beat-phenomenon.html [2] 航天器火箭发射拍振现象假定两组波，圆频率分别为ψ1和ψ2的两组波，表达式如下：
$${\psi _1}(0,t) = Acos({\omega _1}t) = Acos(2\pi {f_1}t)$$
$${\psi _2}(0,t) = Acos({\omega _2}t) = Acos(2\pi {f_2}t)$$
叠加后的波表达式如下
$$\psi = {\psi _1} + {\psi _2} = A[cos({\omega _1}t) + cos({\omega _2}t)]$$
根据三角恒等式（trigonometric identity），进一步转化为如下的形式
$$\psi = \{ 2Acos[({{{\omega _1} – {\omega _2}} \over 2})t]\} cos[({{{\omega _1} + {\omega _2}} \over 2})t]$$
进一步将频率写成均值\({\omega _0}\)与偏差\({\Delta \omega }\)的形式，如下
$${\omega _1} = {\omega _0} – {{\Delta \omega } \over 2}$$
$${\omega _2} = {\omega _0} + {{\Delta \omega } \over 2}$$
于是，可进一步将将叠加后的振动写成如下形式
$$\psi = \{ 2Acos({{\Delta \omega } \over 2}t)\} cos({\omega _0}t)$$
上式是两个cos函数相乘，由于假定两个频率相差特别小，因此均值\({\omega _0}\)远大于偏差\({\Delta \omega }\)，于是第一项三角函数可以认为是第二项三角函数的一个幅度值，且是一个周期变化的幅度值，形成连续的波峰和波谷。
由于\(cos({{\Delta \omega } \over 2}t)\)的波峰和波谷，均是对应极大值，因此拍的周期是\(cos({{\Delta \omega } \over 2}t)\)函数周期的一半：
$${T_{beat}} = {1 \over 2}({{2\pi } \over {\Delta \omega /2}}) = {{2\pi } \over {\Delta \omega }} = {1 \over {|f1 – f2|}}$$
拍的频率则为两个频率之差：
$${f_{beat}} = |f1 – f2|$$
根据文献2的解释，拍振有以下特性，我们直接摘抄下来：
- 当频率比满足0.85≤ξ≤1.18，振幅比满足0.33≤β≤3，两个分振动可合成拍频振动，初始相位差对拍频振动并无实质性影响；
- 频率比影响合成振动振幅周期；
- 振幅比越小，振动的对比度越小，拍振现象越不明显。当振幅比为1时，拍振现象最明显。
我们这里不再进行细致的理论分析，我们通过编写实际案例来看一下效果。
例子1：A1=A2 =1, f1=10Hz, f2 = 10.5Hz，频率比f2/f1= 1.05，振幅比1，根据上面的分析可知，可形成拍振，拍振周期是2s。
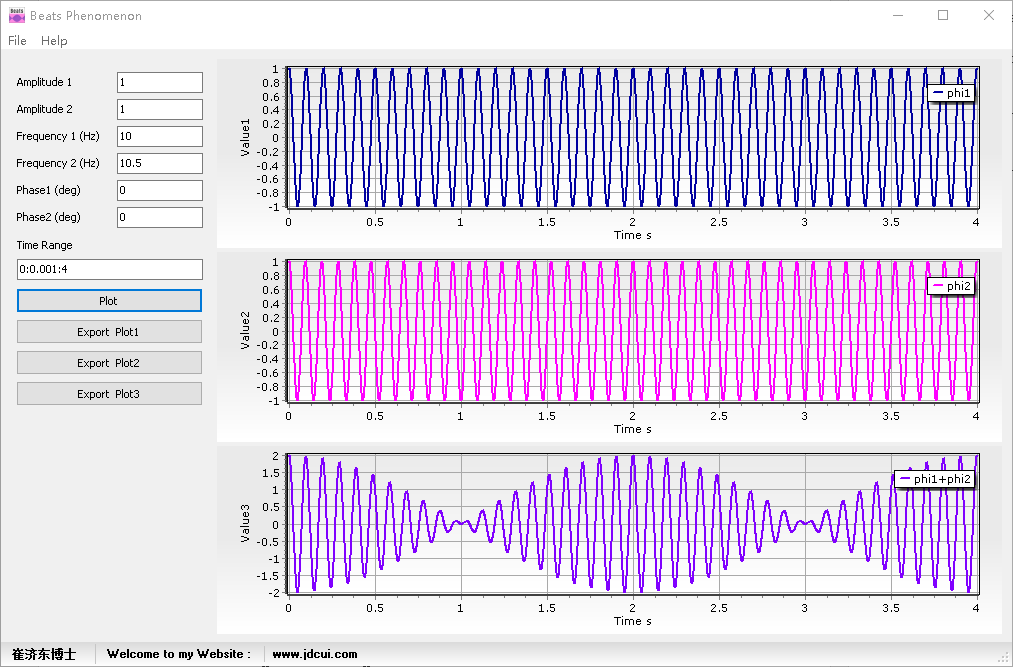
例子2：A1=A2 =1, f1=10Hz, f2 = 11Hz，频率比f2/f1= 1.1，振幅比1，根据上面的分析可知，可形成拍振，拍振周期是1s。
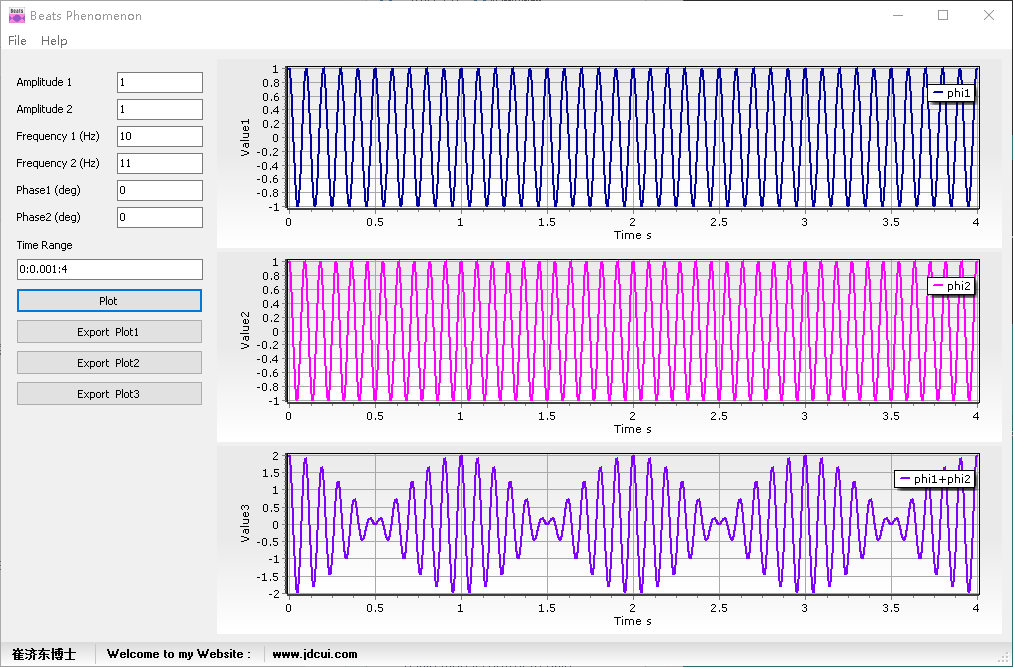
例子3：A1=1, A2 =3, f1=10Hz, f2 = 11Hz，频率比f2/f1= 1.1，振幅比3，根据上面的分析可知，可形成拍振，拍振周期是1s，同时与例子2比，拍振现象没例子2强。
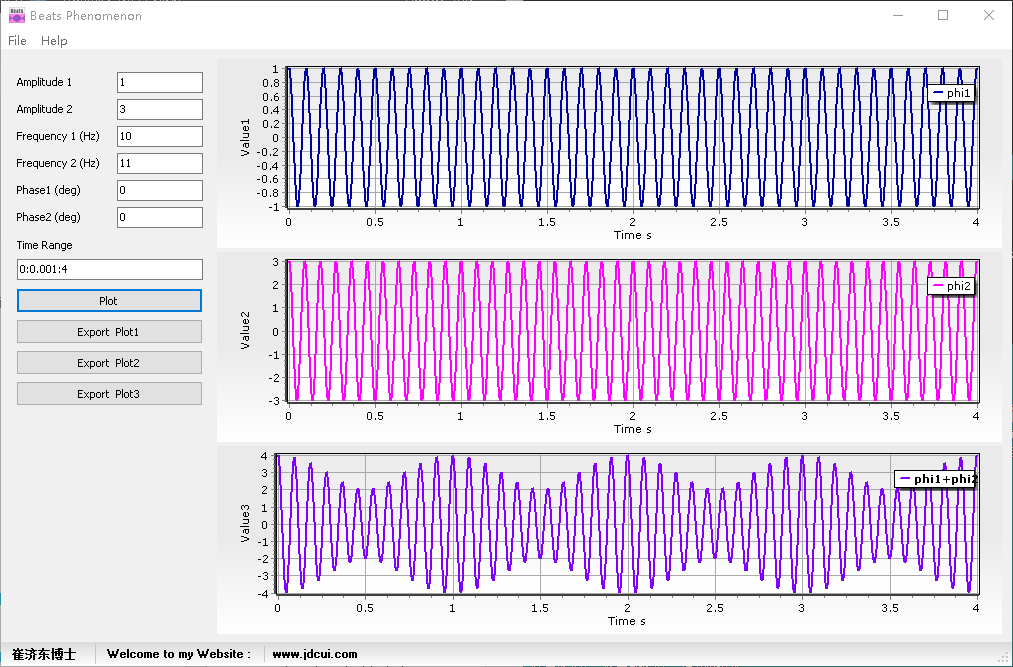
例子4：A1=A2 =1, f1=10Hz, f2 = 13Hz，频率比f2/f1= 1.3，振幅比1，按公式拍振周期是3.3s，但根据上面的分析可知，可知已无明显拍振现象。
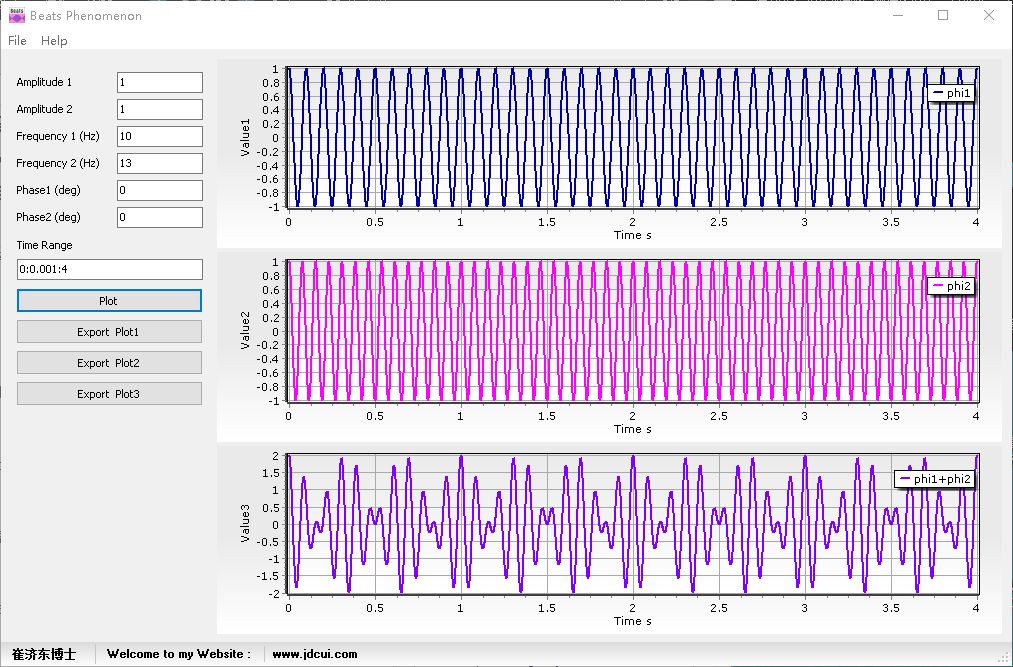
Video 视频演示
- 案例 ( Examples )
[00] [数学][地震动][软件] FOUR_TRAN: Fourier Analysis Tool [傅里叶分析工具]
[01] [数学][软件] FOUR_TRAN Example 1: Filtering [FOUR_TRAN傅里叶分析工具使用案例1: 滤波]
[02] [数学][软件] FOUR_TRAN Example 2: Square Wave Signal Decomposition [FOUR_TRAN傅里叶分析工具使用案例2: 方波信号分解]
[05] [软件] FOUR_TRAN 案例5: 风振响应频谱分析 ( FOUR_TRAN Ex5: Wind induced vibration response spectrum analysis)
[08] [振动控制] 拍振现象 (Beats Phenomenon)
结构|超限|软件开发|编程|参数化|优化|算法|振动控制|减隔震|有限元|技术培训
追求卓越 脚踏实地 致力于探索和拓展行业设计前沿
https://www.jdcui.com
合作及技术咨询
COOPERATION & CONTACT
E-mail：jidong_cui@163.com
WeChat & Tel: 13450468449
