实干、实践、积累、思考、创新。
基于BESO的拓扑优化设计与数字未来工作营分享
大家好,我是Ely,郑依力,今天想和大家分享的是我在前段时间参加同济大学举办的Architectural Digital Futures (ADF)工作营的学习见闻,其中包括BESO在拓扑优化设计中的应用和数字未来工作营的收获。

目录
第一部分介绍编者参加工作营前的准备工作,了解并学习ESO和BESO的相关理论知识;
第二部分介绍编者参加Emerging Form工作营的情况以及编者所在小组的设计作品[Re]forming the cave;
第三部分介绍编者在参加工作营时参观平行工作营的工作或听取有意思的讲座;
第四部分分享编者对此次学习的思考与感恩。
C1 ESO&BESO介绍
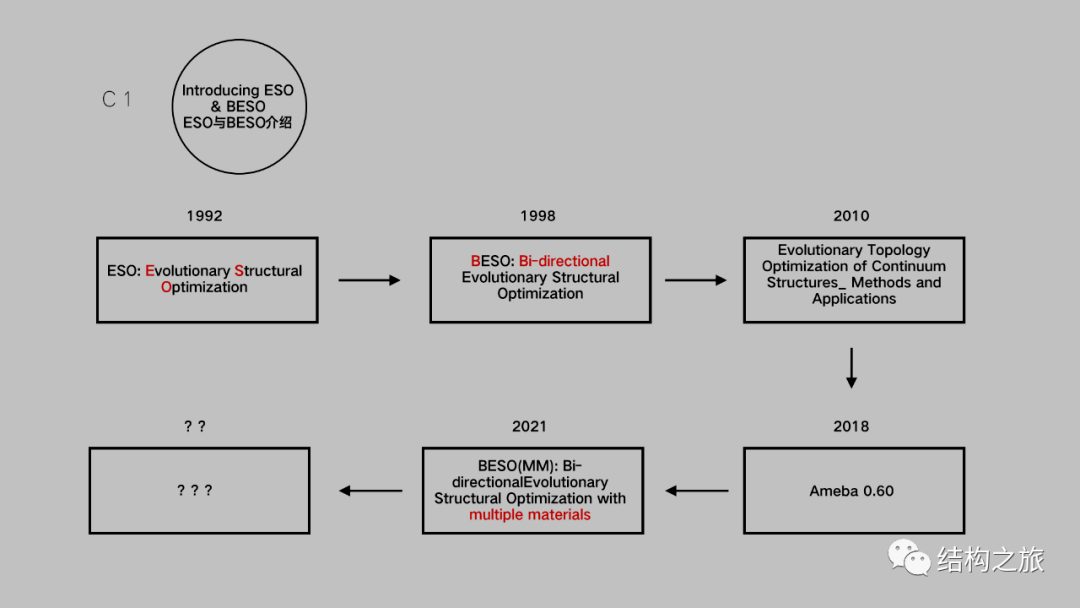
目前我们常说的BESO算法经历了较长时间的发展,期间有众多学者、研究人员参与其中,对该算法进行更新、迭代、改进。BESO的前身可以追溯到ESO,ESO是这三个单词Evolutionary Structural Optimisation的首字母。编者选取了BESO发展史上的一些重要节点,大致介绍其发展脉络。
1992年,Y. M.Xie & G. P.Steven 在Computers & Structures发表了论文 A simple evolutionary procedure for structural optimization 首次提出了 ESO优化方法。其核心概念是通过逐渐迭代,删除低应力单元,使最终结构型体达到最大刚度状态。
1998年,O.M. Querin, G. P.Steven & Y. M.Xie 在Engineering Computations 发表了论文Evolutionary structural optimisation (ESO) using a bidirectional algorithm 首次将ESO方法与双向算法(bidirectional algorithm,BESO的B就来源于bidirectional的首字母)结合,其核心概念是ESO删除低应力单元的基础上,增加一个补充机制,让结构可以恢复部分被删除的单元,从多个维度寻找最优的结构型体。
2010年,X. Huang & Y.M. Xie 发表专著 Evolutionary Topology Optimization of Continuum Structures: Methods and Applications 系统总结了ESO和BESO。
2018年,谢亿民科技把BESO算法整合,基于Rhino-Grasshopper平台推出Ameba 0.60。最近推出了最新的2.2.0版。
2021年,Y,Li & Y. M.Xie, 在Composite Structures发表了论文 Evolutionary topology optimization for structures made of multiple materials with different properties in tension and compression 提出了多材料拓扑优化的方法。
未来我们拭目以待。

渐进结构优化法,也叫ESO方法,最早由谢院士和Steven在1992年提出。ESO方法的原理非常简单,即通过逐渐进化的方式从结构中去除低效材料。
在这篇论文的Introduction部分,作者介绍了ESO算法的灵感来源于自然结构的进化:By observing the evolution of naturally occurring structures such as shells, bones and trees it becomes obvious that the topology and shape of such structures achieve their optimum over a long evolutionary period and adapt to wharever environment they find themselves in.
该论文对ESO算法并没有明确提出优化问题的三要素:决策变量、目标函数和约束条件,编者按照理解从论文的 A simple evolutionary procedure部分提取了潜在的目标函数与约束条件,供读者参考。
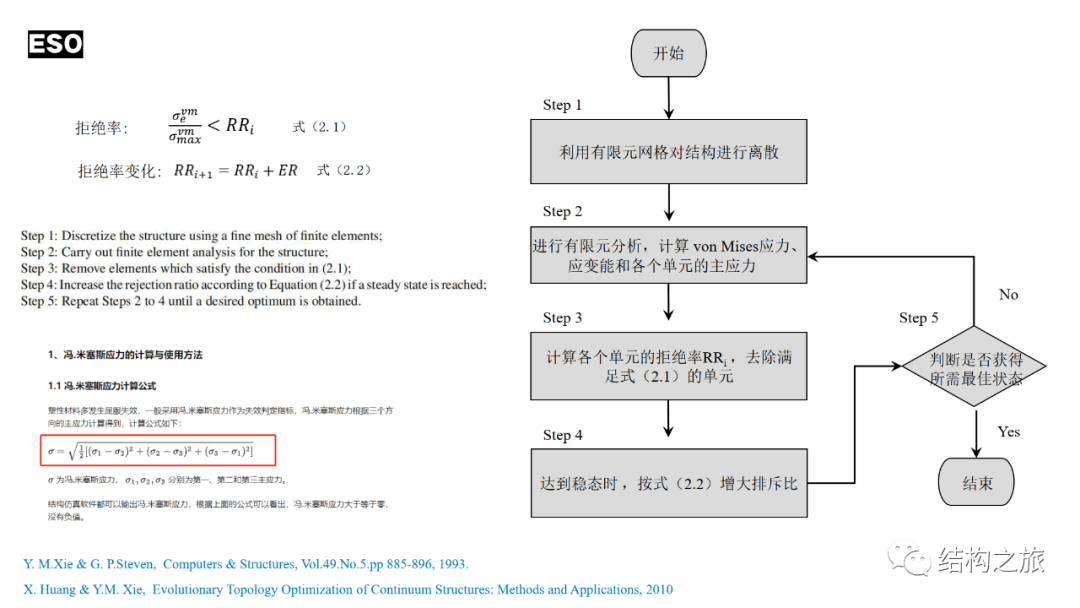
以下是编者根据黄教授与谢院士的Evolutionary Topology Optimization of Continuum Structures: Methods and Applications 中归纳的优化步骤做的翻译。
步骤1: 利用有限元细网格对结构进行离散;
步骤2: 对结构进行有限元分析;
步骤3: 去除满足条件式(2.1)的单元;
步骤4: 达到稳态时,按式(2.2)增大排斥比;
步骤5: 重复步骤2至4,直至获得所需的最佳状态。
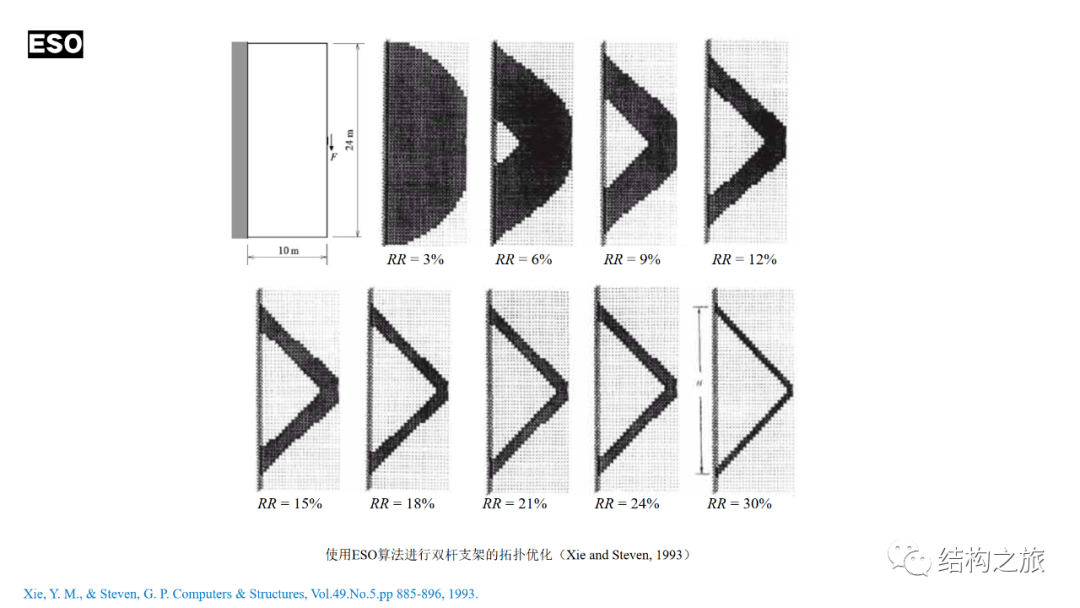
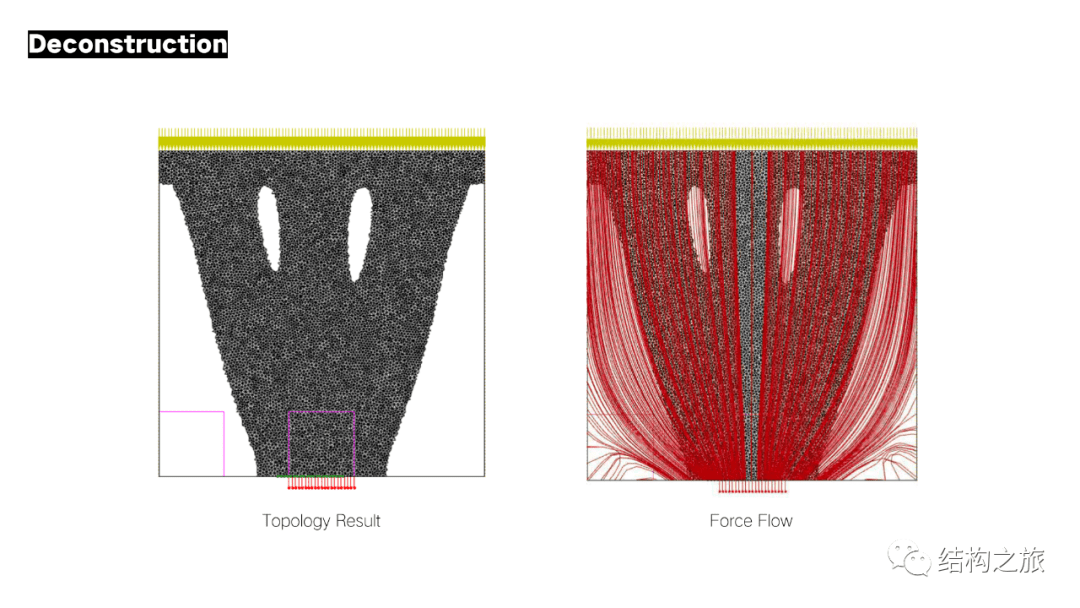
上图展示的是基于ESO算法对一个受集中力作用的2D支架进行了拓扑优化。经过若干步的材料删除之后,得到双杆支架的简洁形态。

1998年,O.M. Querin, G. P.Steven & Y. M.Xie 在Engineering Computations 发表了论文Evolutionary structural optimisation (ESO) using a bidirectional algorithm 首次将ESO方法与双向算法结合,其核心概念是ESO删除低应力单元的基础上,增加一个补充机制,让结构可以在高应力单元附近恢复部分被删除的单元,减轻高应力单元的负担,从多个维度寻找最优的结构型体,优化的结果会从局部最优向全局最优进行探索。这里编者把它归纳为BESO(early),属于早期的BESO算法。

这篇论文里除了给出了单元删除机制RR外,还给出了单元补充机制IR。论文提供了IR和RR的计算公式,但从各个符号的含义和取值看,RR和IR的计算数值存在较强的人为因素,与结构的关联性较弱。虽然判断方式存在缺陷,但这篇论文所提出的补充机制的思维为ESO开辟了新的探索思路,成为了BESO的开端。学者们的研究工作并没有止步于此,对这个问题的继续探索与完善,最终提出了我们即将介绍的soft-kill BESO。

在ESO方法的基础上,谢亿民等人进一步改进了这种算法,提出了双向渐进结构优化(BESO)算法,该算法允许在拓扑优化中同时增加和删除材料,进一步完善了渐进结构优化法的理论完整性。
2008年,X. Huang & Y.M. Xie 在Computational Mechanics发表论文Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials 。
2010年,X. Huang & Y.M. Xie 发表专著 Evolutionary Topology Optimization of Continuum Structures: Methods and Applications 系统总结和归纳了BESO。
明确了以柔度C为目标的函数,以预设体积V*为约束条件。在敏感数的方程中设置了惩罚系数p来衡量删除单元的彻底程度,敏感数ɑi从计算公式上看其实表示的是单元应变能。
Xi是一个二元数,只代表2个值:1或者Xmin(Xmin是一个很小的数,可以想象为0.0001,但不为0),Xmin的设置尤为具有开创意义,它巧妙的使算法具备删除单元却又具备恢复该单元的功能。当Xi=1时,该计算单元保留;当Xi=Xmin,该计算单元会落入删除单元的序列,但不会马上被删除
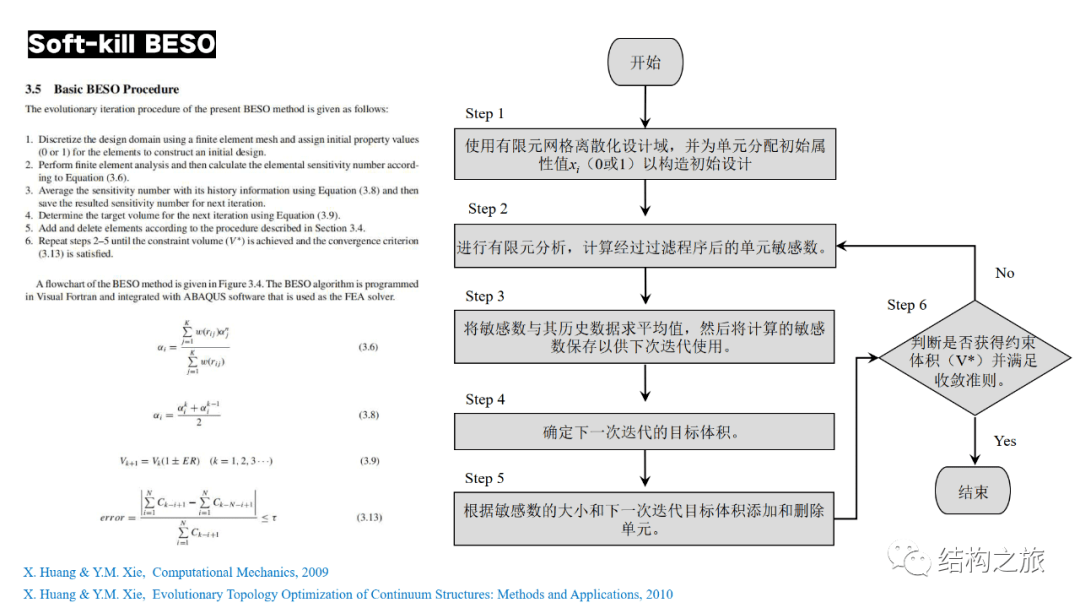
观察步骤Step3,当Xi=Xmin,该计算单元会落入删除单元的序列,但该计算单元的敏感数会求历史平均,再根据历史平均的敏感数ɑi判断是否真正永久删除该单元。
我们观察式1.2可知,当P趋于无限大时,式1.2等于0,即ɑi=0,这就出现了敏感数计算的特解,作者把这种情况称为Hard-kill,即该情况下单元删除更彻底。其余Xi=Xmin的情况称为Soft-kill,即该情况下单元删除不是那么彻底。
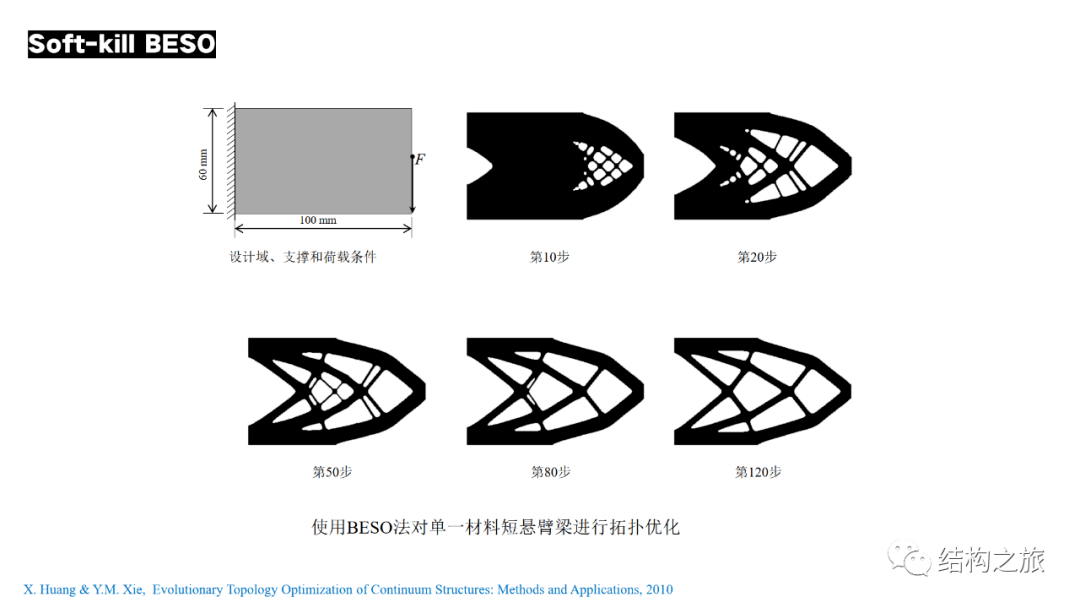
上图展示的是使用BESO方法对单一材料短悬臂梁进行拓扑优化的过程。

2021年,Y,Li & Y. M.Xie, 在Composite Structures发表了论文 Evolutionary topology optimization for structures made of multiple materials with different properties in tension and compression。
由论文标题可知,作者基于单元拉压特性的判断提出了多材料拓扑优化的方法,主要是基于单元的应力张量的第一不变量,也即三个主应力之和确定的,该数值大于0表示受拉,小于0表示受压。

首先作者分析了一个2D的简支梁的受力状态,经过有限元分析可知,该简支梁上部主要受压,下部主要受拉。在这样既有受拉部分又有受压部分的结构中,如果仅仅使用混凝土这种受压性能良好而受拉性能较差的材料进行建造,结构的安全性则无法保证。
所以这里的想法是如果使用两种材料,一种受拉性能较好的材料只负责受拉,另一种受压性能较好的只负责受压,则可以组成高效的组合结构。
为了获得这种拉压组合结构,这里对材料的性能做了几个假设:
1. 两种材料是各向同性的;
2. 结构是线弹性小变形的;
3. 两种力学性能截然不同的材料分别适合受拉和受压
4. 两种材料之间的边界牢固连接的,可以有效的实现不同材料之间力的传递
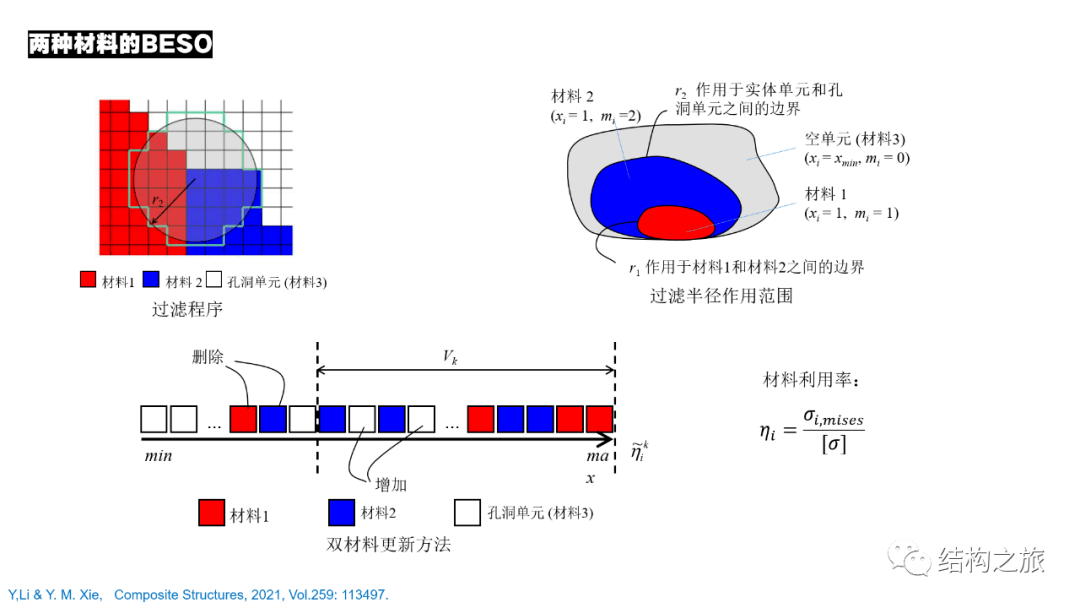
此外,和单一材料拓扑优化方法一样,在多材料结构的拓扑优化中,也是需要使用过滤程序以消除棋盘格图案。这里设置了两个不同的过滤半径分别作用于实体单元和虚单元之间的边界以及不同材料也即材料1和材料2之间的边界。
然后依照材料利用率,也即Mises应力和许用应力的比值进行单元的排序和更新。
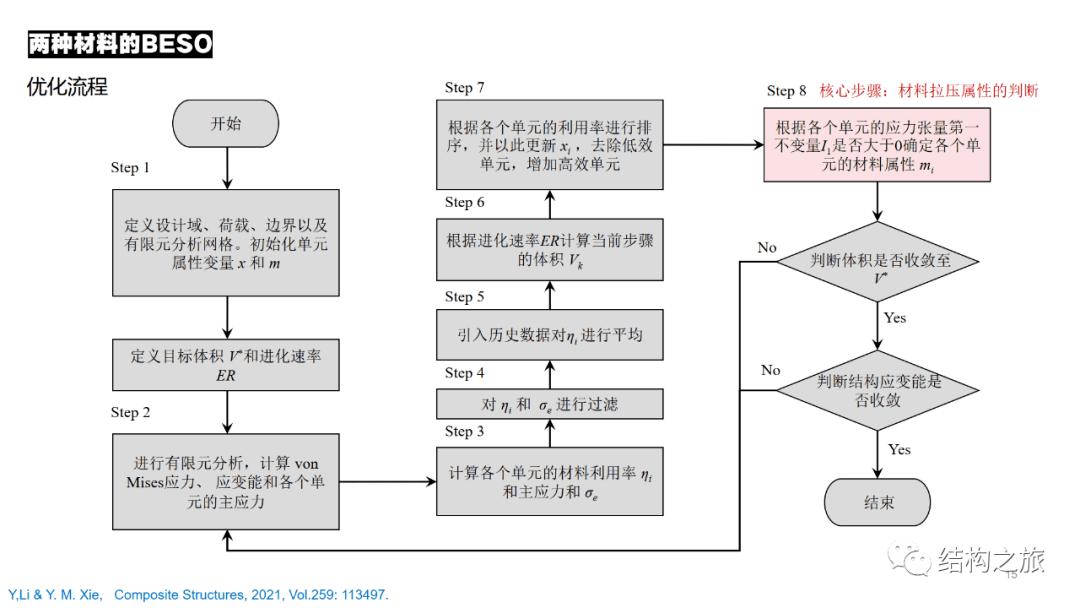
完整的计算流程如图所示,相比于经典的单材料双向渐进结构优化法,比较明显的区别是第8步根据各个单元的应力张量第一不变量是否大于0确定各个单元的材料属性。
迭代循环,直至结构的体积和平均应变能均收敛至稳定值。
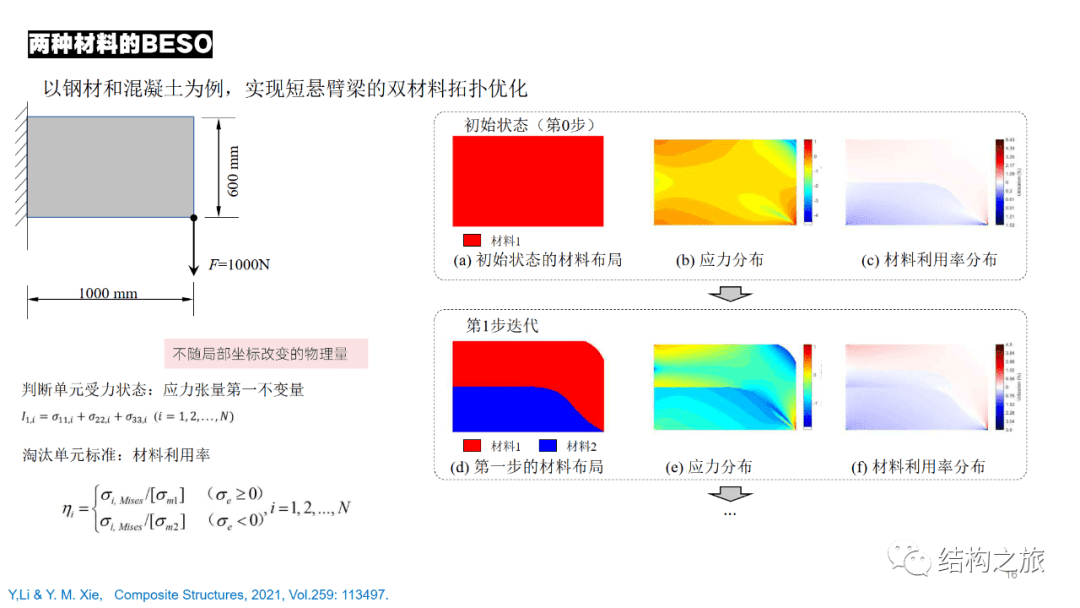
以二维的受集中力的短悬臂梁为例。在初始状态下,设计域内只分配一种材料。通过有限元分析,得到应力分布,并根据应力张量第一不变量将结构分为受拉区和受压区。
接着对受拉区和受压区分别分配适合受拉的材料和受压的材料,例如钢材和混凝土这两种材料。同时删除掉部分低效的单元,从而完成第一步的迭代。
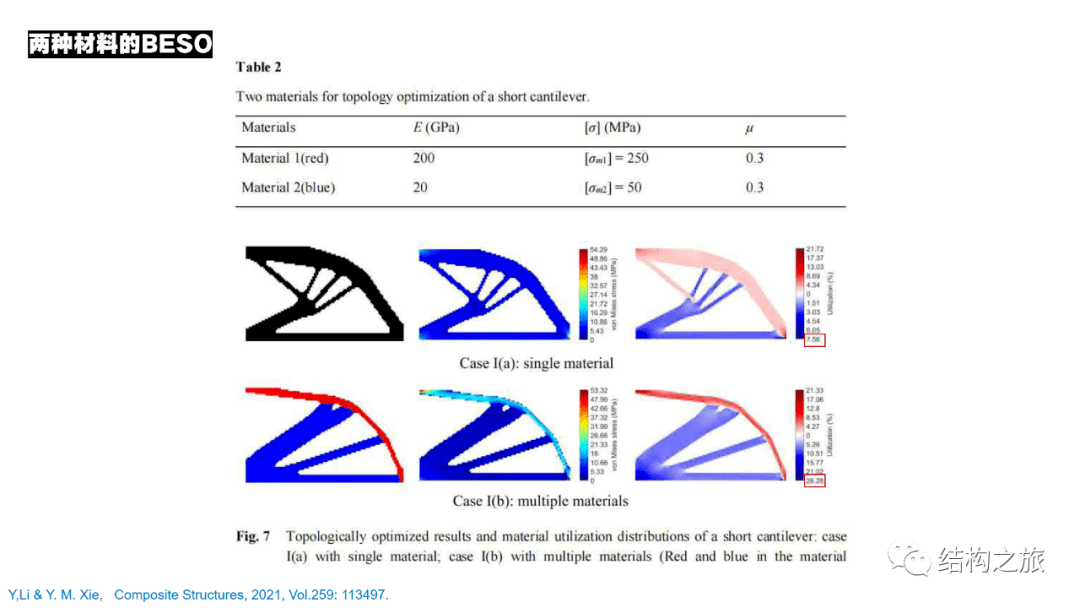
对于单材料和多材料的拓扑优化结果,在结构形态和材料利用效率上都有区别。
感谢 李瑜博士,崔济东博士对第一部分内容的校对斧正!
C2 Emerging Form -> Reforming the cave
编者完成准备工作后奔赴上海,开始工作营的学习。

编者参加的工作营名称为浮现成形,Emerging Form。主要内容是基于拓扑优化的结构设计。

导师阵容:谢亿民、鲍鼎文、严鑫

整个2023年工作营共28个

编者工作营的导师在分享拓扑优化设计的原理、历史及案例。
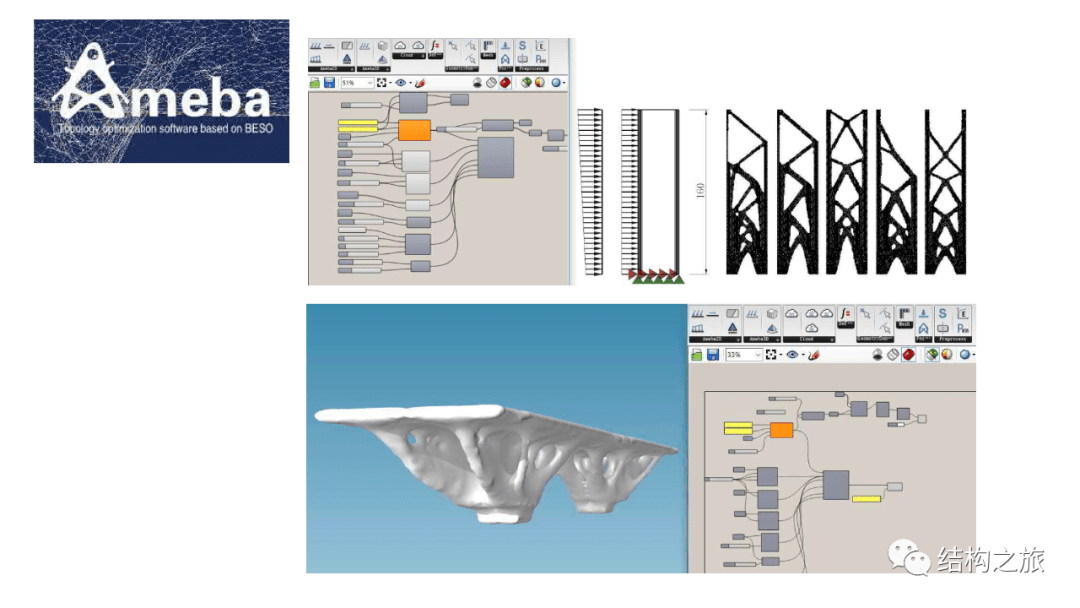
主要应用软件为Ameba

深圳中信金融中信,外立面桁架造型与拓扑优化的形态类似

卡塔尔国家会议中心,“锡德拉树”造型与3D拓扑优化的结果接近,该项目是3D拓扑优化结合实际工程的伟大尝试,从造型不规则的节点图片我们可以感受到金钱的味道。

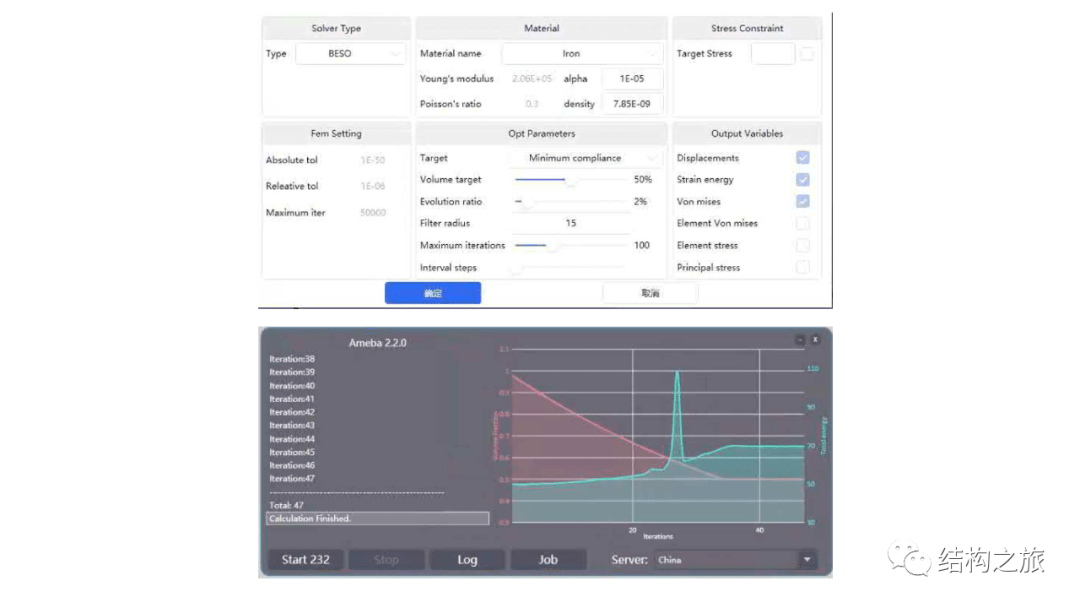
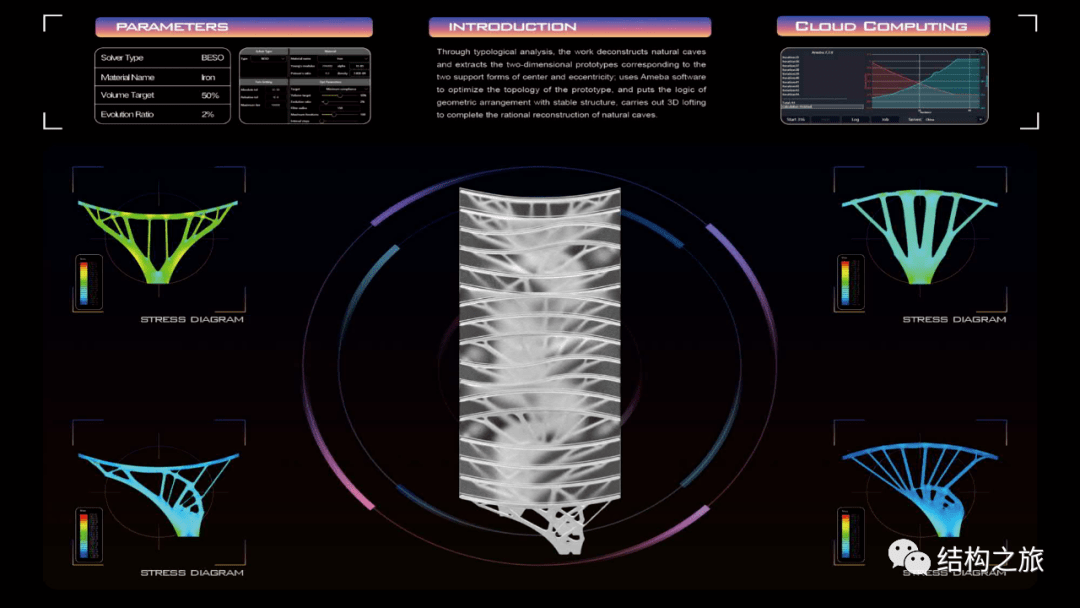
在Ameba2.2的计算设置界面,我们可以看到第一部分介绍的Volume target, Evolution ratio, Filter radius等参数
在Ameba2.2的计算界面中我们可以看到总的迭代次数,红线代表了结构体积,蓝线代表结构总能量,两者最终都趋于收敛。
下面展示编者及组员在工作营共同创作的作品




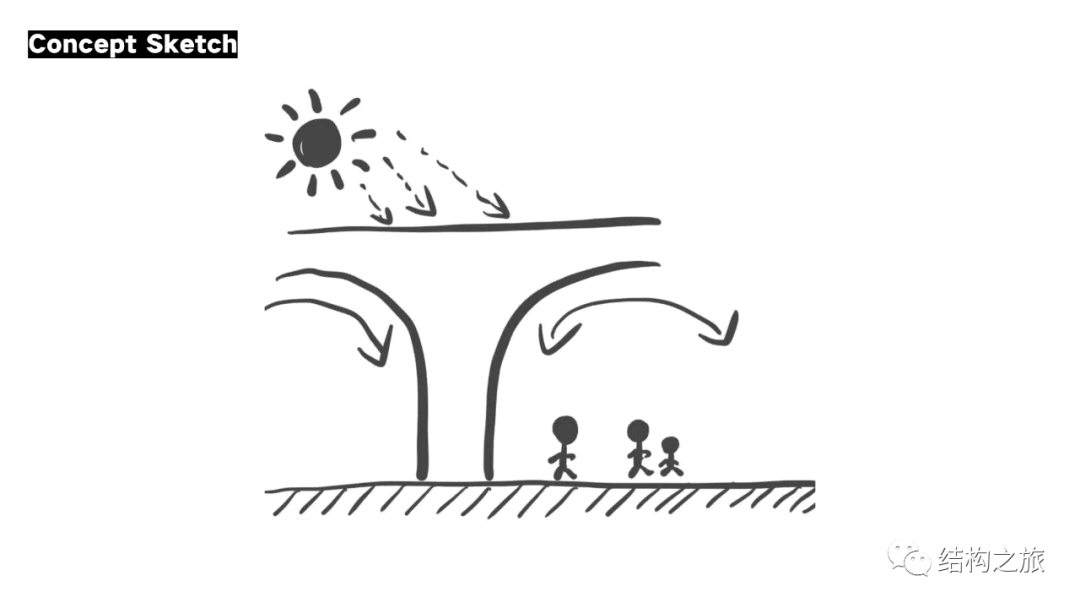
城市中荫蔽空间的建构灵感来源于洞穴对人类的庇护作用。随着时间流逝,自然不断侵蚀,洞穴逐渐消减同时产生沉积的循环成形过程,与双向渐近结构优化法(BESO)的作用原理殊途同归。作品通过类型学分析,解构天然洞穴,提取出正心、偏心两种支撑形式所对应的二维原型;运用Ameba软件对原型进行拓扑优化,并置入结构稳定的几何排列逻辑,对其顶面进行三维放样,完成对天然洞穴的理性重构。作品以上海外滩为背景,探讨未来城市中荫蔽空间的新兴建构策略,呈现出兼具人文性与前瞻性的“人造洞穴”图景。
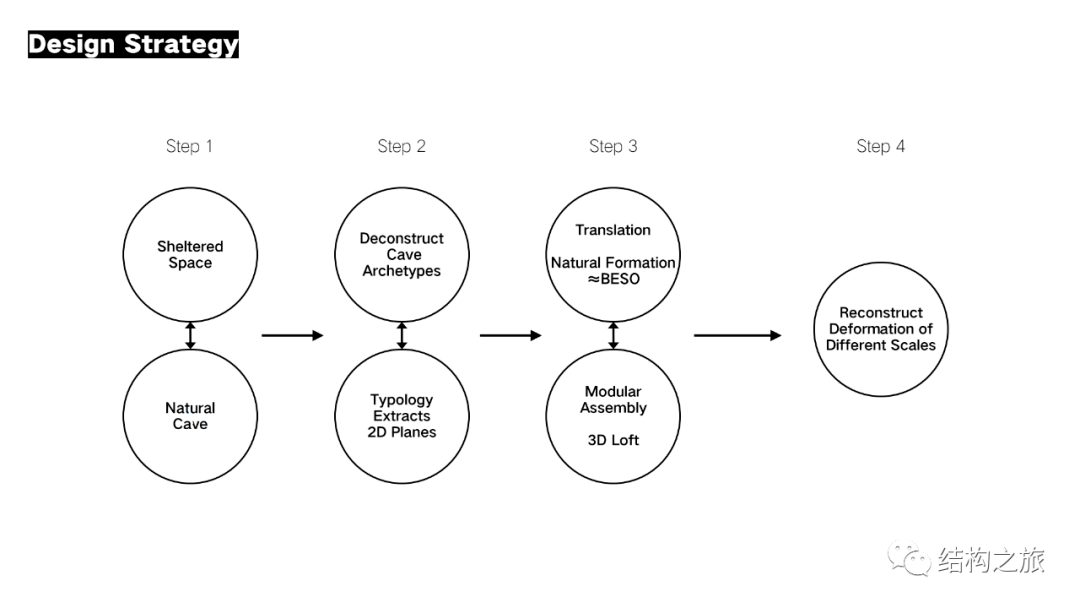
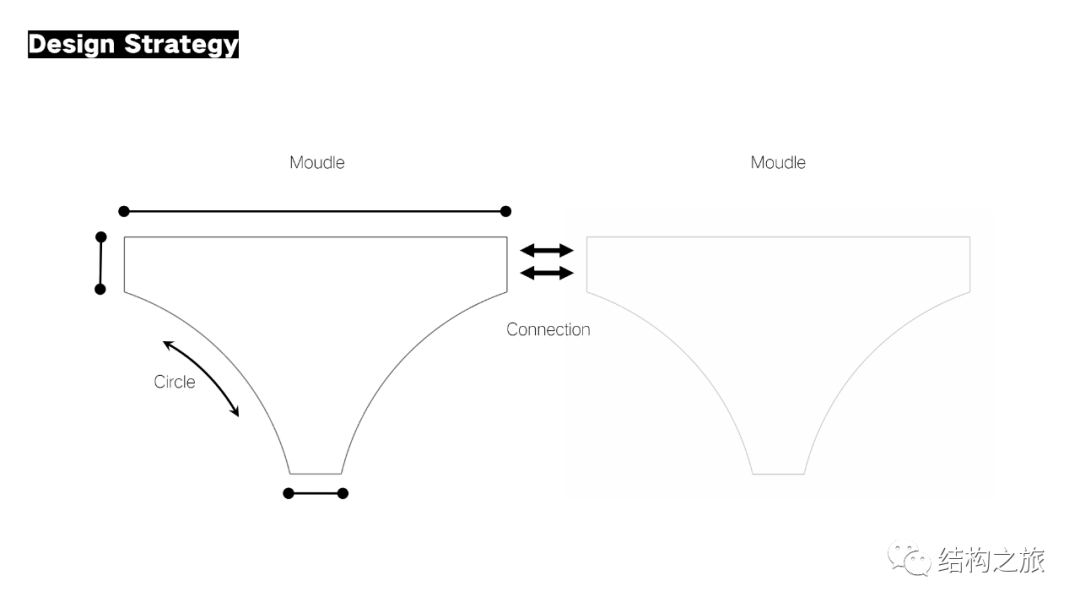
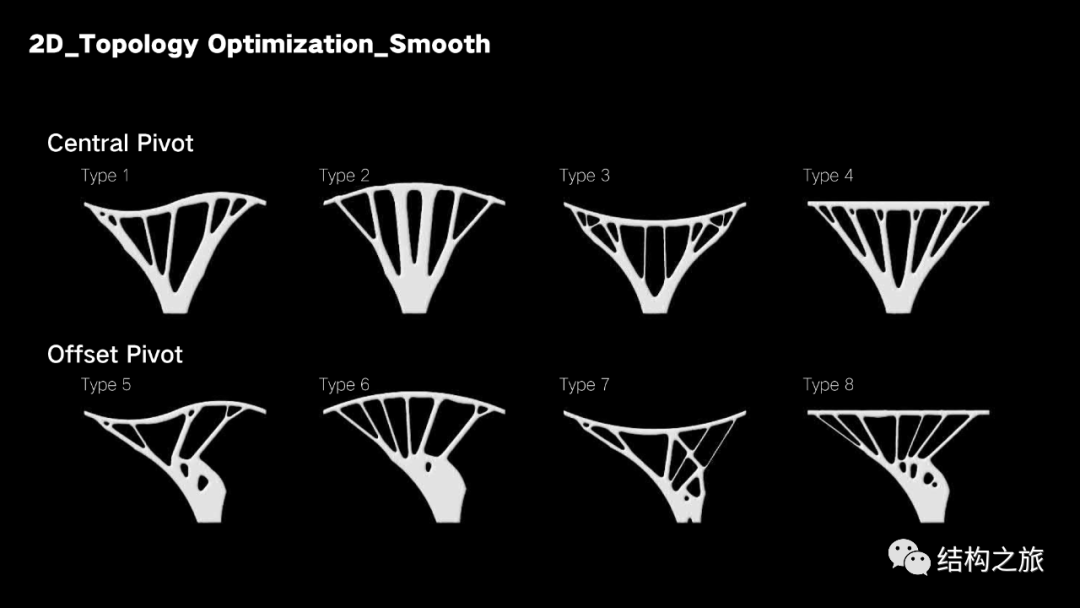
解构:编者从一个长方形开始,在只设置顶面均布荷载+底面中部约束的条件下对长方形进行拓扑优化,得到了类似洞穴支撑的原型
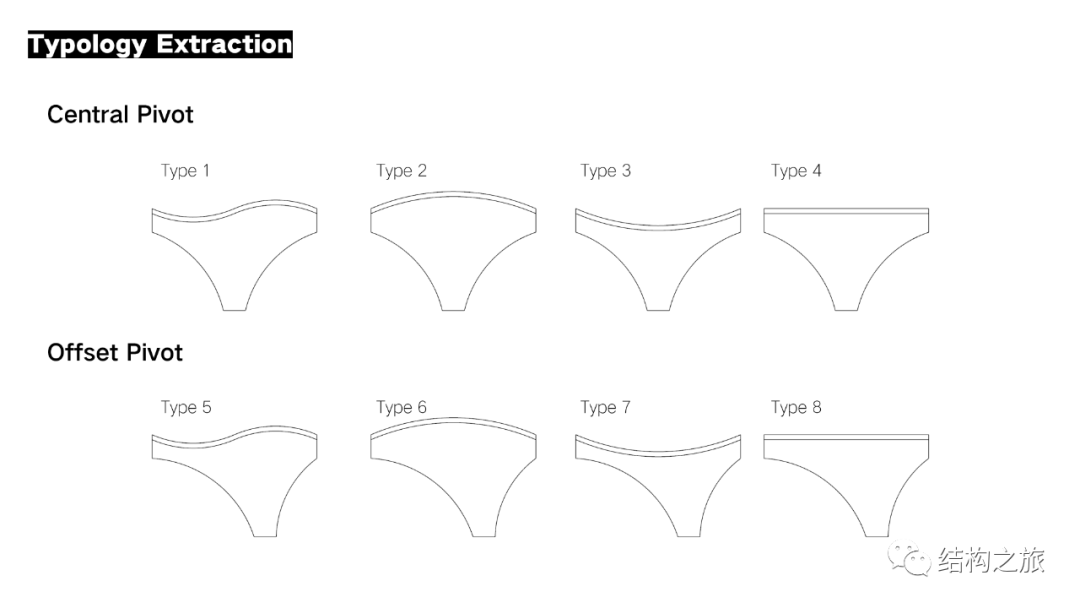
分类:对提取的8个原型,分为对称和偏心两类
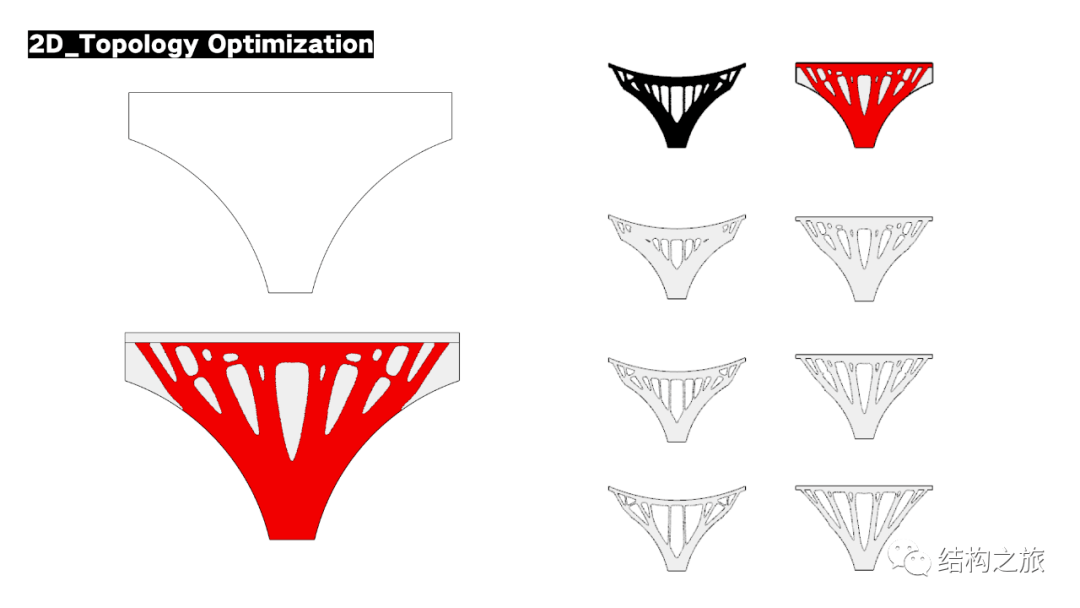
对8个原型进行拓扑优化,并得到其在80%、60%、40%结构体积下的优化结果
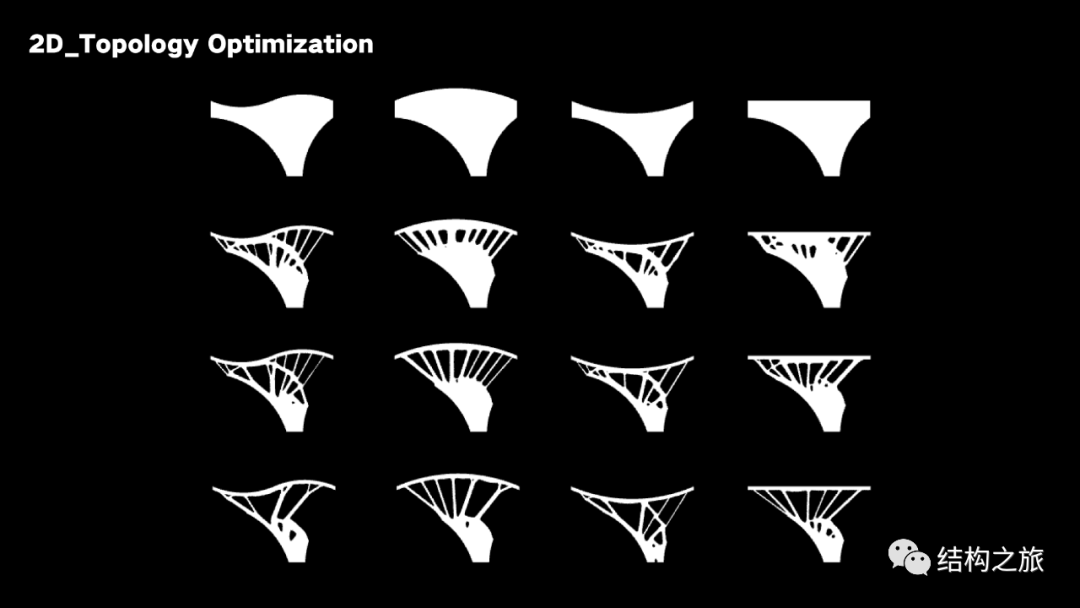


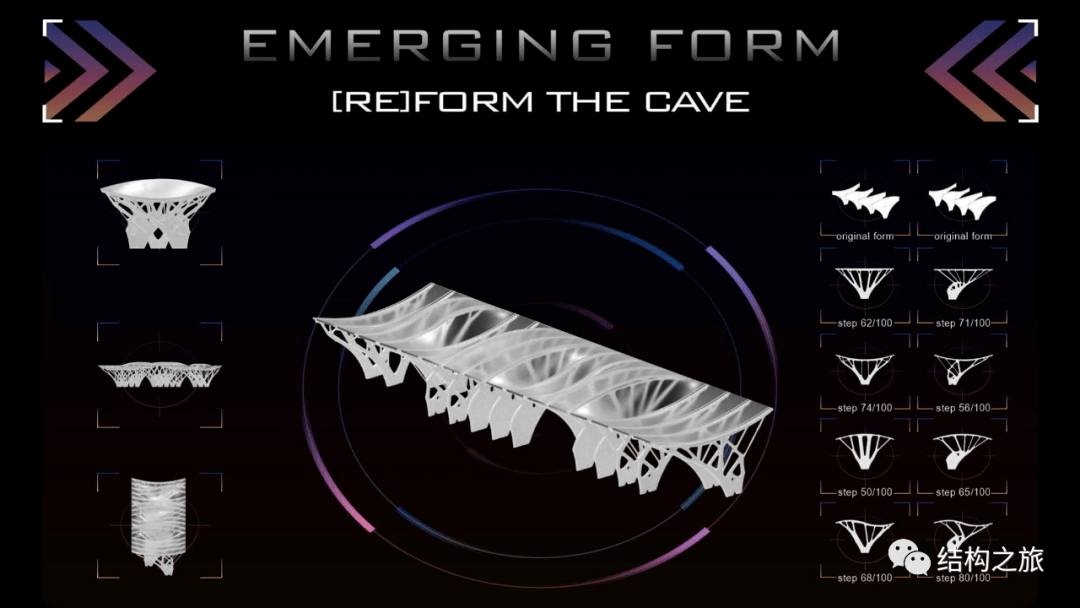
重构:基于8个支撑原型,进行有机的排列重构

最终作品三维图。

由于上海外滩没有遮蔽空间,编者及团队希望能为来到这里的游客增加一些基于自然元素的庇护场所。


感谢workshop导师: 谢亿民院士、鲍鼎文博士、严鑫博士的悉心指导。
感谢编者所在的workshop团队: 张子希,傅逸舟,王佳奇
C3 Parallel Workshop sharing 平行工作营分享

在Workshop期间,有很多不同课题的workshop在平行开展,包括Philippe Block 教授(ETH)的编织网壳,CarloRatti 教授(MIT)的Smart CLT,袁烽院长(同济)的空间骨架轮廓工艺,ZHA Code的面向高性能设计与建造的几何学等等28个有意思的workshop。在工作之余编者参观了部分工作营并听取了部分导师的分享。接下来将与大家分享几个与结构和建造有关的平行工作营。

Philippe Blcok 教授是ETH的大牛

如果大家对Philippe 教授不是很熟悉的话,这个在2021年刷屏建筑圈的作品Striatus应该能唤起大家的记忆。这是展出在2021年威尼斯双年展的纯水泥3D打印步行桥,由ZHA Code与Philippe教授领导的ETH-Block Research Group(BRG)合作完成。在6月29日的演讲中,Philippe教授与我们分享了这个作品的设计与建造的点滴。

Striatus桥面构建正在打印

Striatus构件打印细节

Striatus安装中,从细节图看打印的精度非常高

Striatus的满堂支架及现场安装
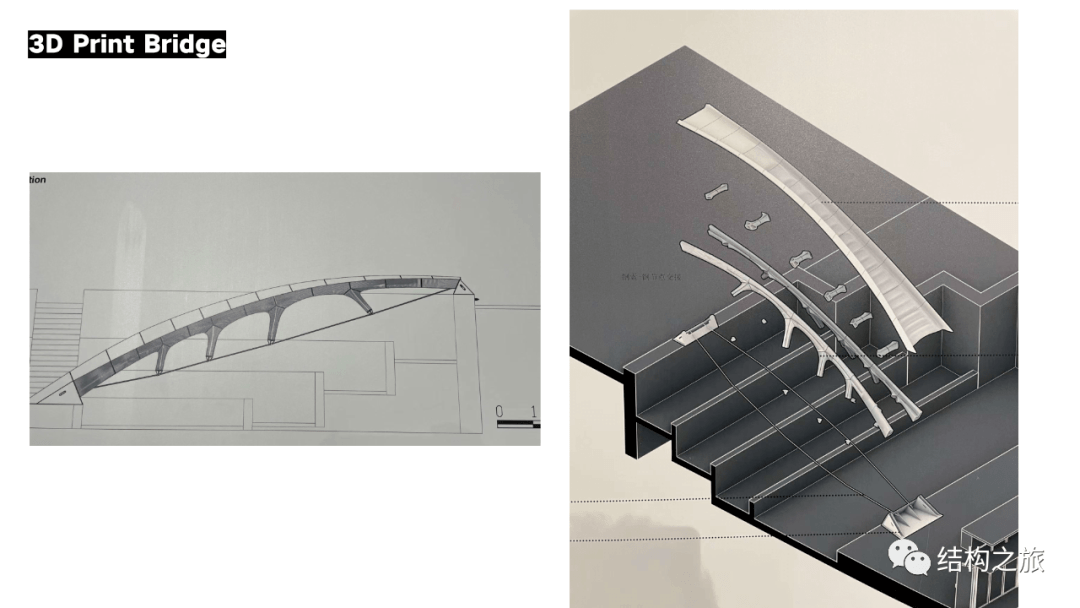
袁烽院长团队也在同济现场尝试建造一个张弦结构的纯水泥3D打印步行桥

工人在焊接桥体

桥体节点。
从现场拍摄的节点图可以看出,节点连接位置采用了预制钢埋件的做法,现场工人通过钢埋件焊接。
转折位置的打印有些粗糙。

桥体在满堂支架上拼装

但是很不幸的是桥体在主体安装完毕开始铺设桥面的当天发生了意外。

编者在桥体出现意外的位置观察,现场已安装了预应力索并拆除部分支撑,初步判断可能有两个引起桥体坍塌的原因。
1. 可能存在预应力索加载未完成取消了支架导致桥体塌陷。桥梁的形式是张弦结构,下部预应力索的加载尤为重要,预应力索加载完成后,索将对桥体提供竖向约束并将竖向力转为索的拉力,最终传至支座。若果索未完成加载,那么将无法承受桥身的竖向变形,由于打印桥体为纯水泥3D打印,水泥本身抗拉性能很弱,无法承受过大的竖向变形导致塌陷。
2. 3D打印构件似乎为空腔结构,内部没有设置肋板以提高纯水泥构件的抗剪性能导致结构破坏。从现场图片可见构件的破坏不是发生在节点而是连接节点以外的位置,说明节点部分强度满足,主要问题出在非节点区,破坏形式类似受剪破坏(顺打印纹路)。
虽然桥体在展览日前发生了坍塌,所幸没有人员受伤。首先这确实是3D打印的先锋尝试,相信一次失败的经验会比成功的经验更有价值,只要通过合理复盘与改进,一定能迎来成功。

视频为编者在体验AR增强现实组指导现场木结构施工工作营的AR眼镜。

左图为AR眼镜中显示的结构,涵盖了需要建造结构的所有信息,而且建造团队可以非常便利的在AR中解构节点构造,了解构件编号、了解构件空间定位等信息,实现更直观的建构过程。
右图为该工作营的最终作品,和AR中的模型对比,完成度非常高。


通过整个工作营的学习,编者完成了自己工作营的工作之余,接触到非常多的学界大牛,与很多来自全球的优秀硕士、博士以及教授一同工作,完成设计。
单纯从工业界、产业界的现实条件来看,很多新兴的前沿的技术,在产品或者设计上应用几乎不可能。
但是从人类发展的视野看,技术的进步永远不会止步,今天的问题不一定是明天的阻碍。
乔布斯推出iphone前,没人知道智能手机能如此改变我们的生活;
ZahaHadid推出fancy 的曲线建筑前,曲线还属于上帝;
参数化技术在21世纪初开始在建筑设计中应用,到目前也并未完全普及;
AI刚开始走进大众视野,还不能完全辅助设计,未来又能如何改变世界?
我们每个人都在经济周期的浪潮里,在人类历史的海面上,在最接近未来的时点中。
困难每个时代都存在,今天的机会并不比昨天少。
问题是我们拥有什么Vision,多少的Passion,怎样Action。
衷心感谢RBS领导及同事的支持,促成编者这次的ADF workshop之旅。
衷心感谢旅程中遇到的每一位导师、友友和陌生人的帮助。

1. 项目终期答辩现场
2. 项目终期答辩现场——编者在回答导师提问
3. 项目成果展团队合影
4. 浮现成形工作营展览

5. 项目团队与导师合影
6. 项目团队与Philippe Block 教授合影
7. 编者与谢亿民院士合影
8. 十三届ADF workshop成员合影


- 微信公众号 ( Wechat Subscription)
欢迎关注 “结构之旅” 微信公众号

