实干、实践、积累、思考、创新。
CSI API编程训练第二课，这次做一个基于虚功原理的伸臂桁架几何优化，主要训练如何通过编程控制SAP2000修改节点位置，自动提交计算分析，并提取构件的内力等。
对于桁架结构，根据虚功原理，结合单位荷载法可知，结构任意一点在指定方向的位移可按以下公式表示：
$${\Delta = \sum {\int {\frac{{n{F_N}}}{{EA}}} } {\rm{ds}} = \sum {\frac{{n{F_N}L}}{{EA}}} }$$
其中，\(n\)为杆件的虚拟轴力，\({F_N}\)为杆件的真实轴力，\(E\)为杆件的弹性模量，\(A\)为杆件的截面面积，\(L\)为杆件的长度。
根据Baker的研究可知，对于静定桁架结构，各杆件处于等应力状态时，结构杆件是最优的。这个最优说的是，对于给定挠度，当所有杆件均处于等应力状态时，所需结构材料用量最小；或者说对于给定材料用量的结构，当所有杆件均处于等应力状态时，结构挠度最小。
假设各杆件的应力水平均达到同一个值，设为\(e = \frac{{{F_N}}}{{EA}}\)，此时结构任意一点在指定方向的位移公式变为以下：
$${\Delta = \sum {\int {\frac{{n{F_N}}}{{EA}}} } {\rm{ds}} = e\sum {nL} }$$
由上述公式可见，当e一样时，\(\sum {nL} \)越小，结构的位移\(\Delta \)越小，结构的刚度越大，此时\(\sum {nL} \)可以看做是一个能量指标，杆件虚拟力与杆件长度的乘积。我们不妨把上述公式中的虚拟轴力换位真实轴力，则\(\sum {nL} \)变为\(\sum {{F_N}L} \)，这就是Baker在另外一篇文章中提到的传力路径，也常称为力流。关于力流，这个文章也介绍过：弘构大讲堂 | 基于力流(∑N ×L)的结构效率评价方法。
对于不同的结构，我们可以利用\(\sum {{F_N}L} \)评估各个结构的几何构型，\(\sum {{F_N}L} \)越小，表明这个几何构型传力越直接，传力路径越短，在构件达到满应力或同等应力水平的条件下，刚度最大。于是可以利用这点，找到静定桁架的最优几何构型。
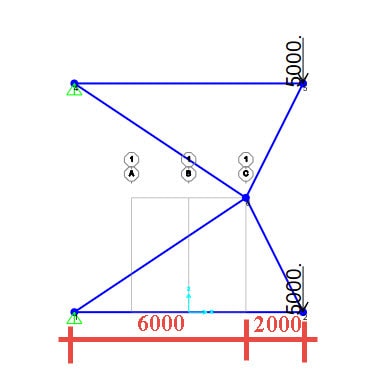
下面我们用一个X型伸臂桁架的几何优化为例进行演示。在SAP2000中进行X型桁架建模，如下图。
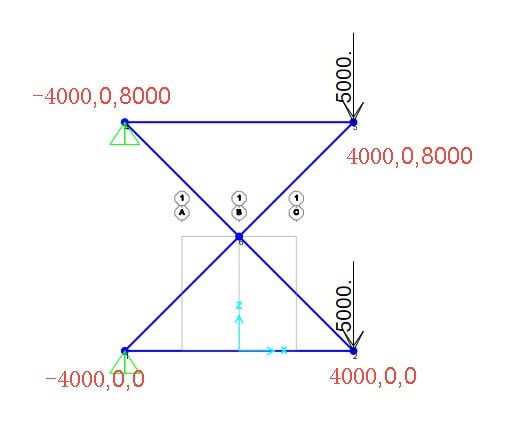
其中X型伸臂桁架的宽、高均为8000，我们通过迭代寻找中间X点的最优位置。
打开小软件，设置控制节点、坐标变化范围、监测点、监测位移和迭代步等参数。
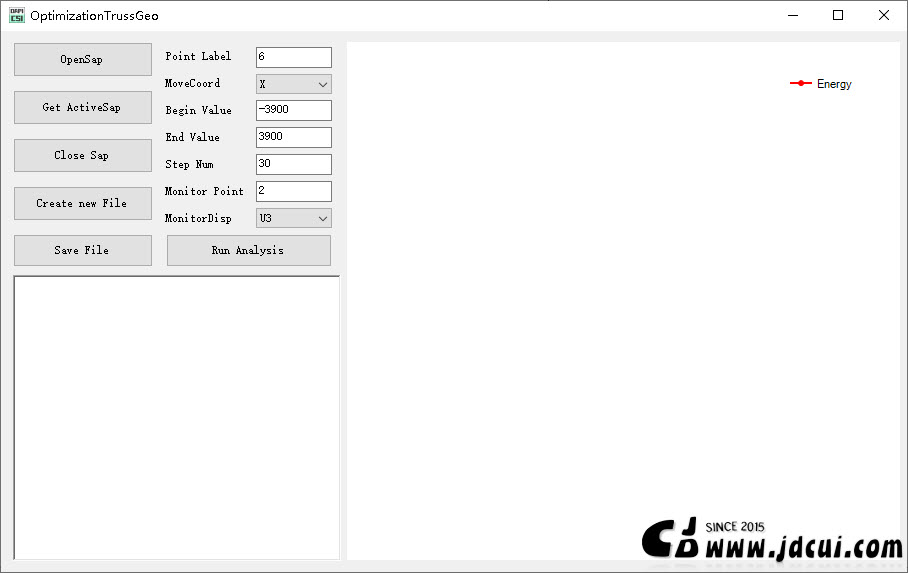
设置好参数后，点击运行分析，软件控制SAP2000进行迭代计算，可以在软件界面看到实时的迭代过程。
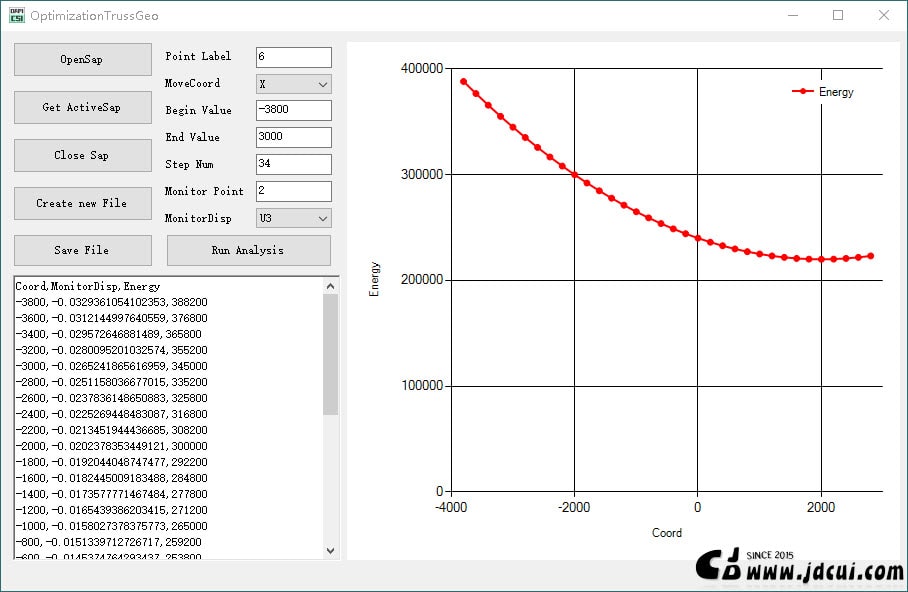
下图是最终分析结果。其中第一个图是迭代坐标和监测点竖向位移的关系，第二个图是迭代坐标和力流 \(\sum {{F_N}L} \)的关系。
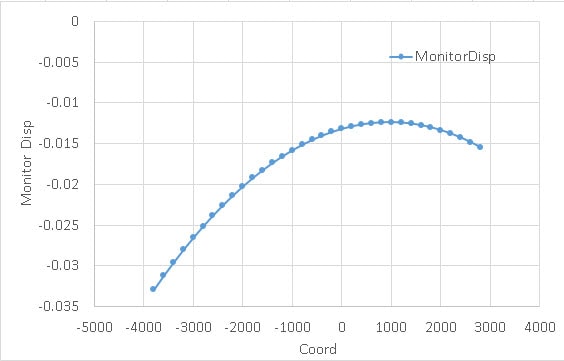
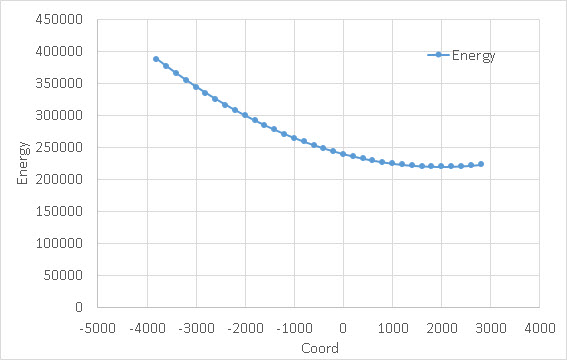
由第一图可以看到，位移最小的X坐标是1000，第二图力流最小的X坐标是2000。
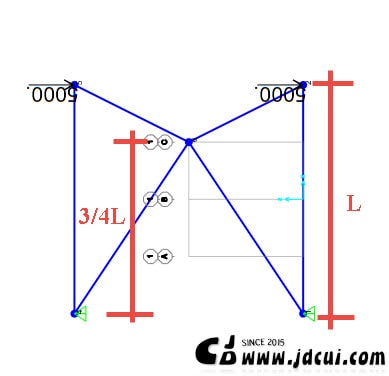
而X=2000才是最优几何构型位置，如下图所示，得到了我们经常看到的3/4位置。
以下是整个软件分析动画。
另外陈学伟博士在 [Dino笔记]伸臂桁架的几何优化方法 中通过Opensees二次开发的方式也做过，大家可以对比看看。
参考文献：
[01] Baker WF. Energy-Based Design of Lateral Systems [J]. Structural Engineering International, 1992, 2:99-102.
[02] Baker WF, Beghini LL, Mazurek A, Carrion J, Beghini A . Maxwell’s reciprocal diagrams and discrete Michell frames [J]. Struct Multidisc Optim. (2013)
- 相关资料 ( Related Topics )
[01] [CSI OAPI][编程] CSI OAPI EX1: 运行/关闭/捕捉 SAP2000 [Start/Exit/GetActive SAP2000]
[02] [CSI OAPI][编程] CSI OAPI EX2: 伸臂桁架几何优化 [Geometric optimization of outrigger truss]
- 微信公众号 ( Wechat Subscription)
欢迎关注 “