实干、实践、积累、思考、创新。
不考虑梁本身的伸长、弯曲等自身变形,单纯考虑水平放置的梁跨中发生挠度 的情况下,水平伸缩量Δ的大小。这其实是一个纯数学的推导,已经和物理无关了(PS. 题目说梁其实不对),其实说的是一根不可伸缩的直线,跨中发生挠度 ,变为两根直线后,水平伸缩量是多大。
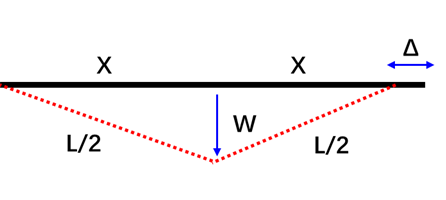
其中 \(L\)为直线的总长度,\(\Delta \)为水平伸缩量的大小,\(X\)为直线发生倾斜变形后,水平投影长度的一半。
由总长不变,可得水平伸缩量
\(\Delta = L – 2X\)
同时 \(L\)、\(\Delta \) 及\(X\) 之间满足以下三角函数关系
\(2X = 2\sqrt {{{\left( {\frac{L}{2}} \right)}^2} – {\omega ^2}} \)
将上式代入第一个公式,可得
\(\begin{array}{l}
\Delta = L – 2X\\
= L – 2\sqrt {{{\left( {\frac{L}{2}} \right)}^2} – {\omega ^2}} \\
= L – 2\sqrt {{{\left( {\frac{L}{2}} \right)}^2}\left( {1 – {\omega ^2}{{\left( {\frac{2}{L}} \right)}^2}} \right)} \\
= L – L\sqrt {\left( {1 – {{\left( {\frac{{2\omega }}{L}} \right)}^2}} \right)}
\end{array}\)
根据泰勒公式 (Taylor formula),可对函数\(\sqrt {1 – x} \)在 \(x{\rm{ = }}0\)处进行展开(即获得麦克劳林公式),并取前两项,当\(x\)为微小量时,有
\(\sqrt {1 – x} \approx 1 – \frac{1}{2}x\)
于是可得,当 \(\frac{\omega }{L}\)是微小量时有
\(\sqrt {\left( {1 – {{\left( {\frac{{2\omega }}{L}} \right)}^2}} \right)} \approx 1 – \frac{1}{2}{\left( {\frac{{2\omega }}{L}} \right)^2}\)
则水平伸缩量变为
\(\begin{array}{l}
\Delta = L – L\sqrt {\left( {1 – {{\left( {\frac{{2\omega }}{L}} \right)}^2}} \right)} \\
\approx L – L\left( {1 – \frac{1}{2}{{\left( {\frac{{2\omega }}{L}} \right)}^2}} \right)\\
\approx 2\frac{{{\omega ^2}}}{L}
\end{array}\)
可见,水平缩短量\(\Delta \)约为\(\frac{{{\omega ^2}}}{L}\)的两倍,当\(\omega \)为微小量时,水平缩短量\(\Delta \)是比\(\omega \)更高阶的微小量。
虽然上面分析的不是一根实际的梁,但从上面的推导也可以发现,对于一些常规的几何非线性可忽略的梁,梁跨中下挠引起的端部水平位移其实是非常小的,大致为\(2\frac{{{\omega ^2}}}{L}\)这个量级。当然,如果计算精确的梁的水平位移,需要建立微分方程的方法来推导,或者开个大变形用FEM计算。
- 相关博文( Related Topics)
[01] [工具][软件][规范] 广东省标准《高层建筑混凝土结构设计规范》反应谱计算工具
[02] [结构力学][结构设计] 两端固支梁弯矩为0点距端部的距离
[03] [抗震][结构设计][规范] 非抗震设计情况下混凝土柱的“轴压比”可达多大?
[04] [结构设计][动力学] YJK中CQC振型组合地震力的复核
[06] [结构][设计][规范] 关于结构倾覆力矩计算公式的另一种理解
[07] [结构设计][规范] 结构整体倾覆力矩及抗倾覆力矩的计算——以YJK为例
[08] [YJK][结构设计] YJK中的地下室侧土侧向约束土弹簧测试
[09] [结构设计][规范] 关于“扭转耦联”、“偶然偏心”、“双向地震作用”的总结
[10] [结构设计][规范] 与“嵌固”相关的规范条文总结
[11] [抗震][结构设计] 规范的各种刚度比”Ratx,Ratx1,Ratx2,RJX1,RJX3″及嵌固层
[12] [抗震][结构设计] 关于“扭转效应明显”与“两个水平方向振型参与系数”
[13] [结构设计] [超限设计] 规范“扭转位移比”的相关条文
[14] [结构设计][地震作用][规范]振型分解反应谱法的一些概念总结 (Basic Concepts of Response Spectra Method)
[16] [钢结构][笔记] 钢梁的局部稳定与腹板加劲肋 (Local Stability of Steel Beam and Web Stiffeners)
[19] [结构设计][超限][工具] “高规”结构抗震性能目标查询工具
[20] [结构设计] 开斜洞剪力墙的受力特性
[22] [抗震设计][结构规范] 如何有效考虑结构在地震作用下的“扭转影响”?!
[23] [抗震设计][结构规范] 规定水平力、倾覆弯矩、振型组合等电算结果的复核总结
[24] [地震][结构] 双向地震作用效应,【先振型组合,再方向组合】及【先方向组合再方向组合】的差异?(实际案例测算)
[25] [规范][结构][设计] 剪力墙边缘构件的尺度问题 (The dimension problem of the boundary element of the shear wall)
[26] [结构][设计][规范] 关于结构倾覆力矩计算公式的另一种理解
[27] [结构][YJK][设计] “一次性加载”、“模拟施工1加载”及“模拟施工3加载”的差别及案例测算 ( Construction Simulation)
[28] [笔记][算例] “剪切型”与”弯曲型”位移曲线的位移角特性
[29] [抗震][结构设计][规范] 非抗震设计情况下混凝土柱的“轴压比”可达多大?
[30] [笔记][结构] 斜柱方案受力分析点
[31] [结构][笔记][材料] 矩形截面与H形截面的抗弯能力 ( Bending Resistance of Rectangular Section and H-shaped Section)
[33] [结构力学][结构设计] 两端固支梁弯矩为0点距端部的距离?
[35] [结构设计][笔记] 钢筋桁架楼承板和压型钢板组合楼板
[36] [笔记][规范][钢结构] 美国规范中的ASD及LRFD
[37] [笔记][算例][减振] 调谐液体阻尼器减震算例 [Example of Vibration Reduction of Tuned Liquid Damper (TLD) ]
[38] [抗震][消能减震] 结构应变能计算公式 (Structural Strain Energy)
[39] [结构力学][笔记] 不同支座条件的斜梁的受力分析(两道结构力学题)
[40] [抗震][动力学] 对于整体结构,X向地震作用下有Y向剪力吗?有!!
[41] [结构][软件] 刚度越大内力越大吗?(单榀框架测算)
[43] 为何结构越长温度效应越显著??
[44] 为何长的橡皮筋比短的橡皮筋更容易拉伸?
[45] [FEM][SteelStructures] 有侧移与无侧移框架的屈曲模态 (Buckling Modes of Frames with and without Sidesway)
[46] [结构][有限元][PFSAP] 平行弦桁架简单算例及概念 ( Basic concepts and examples of parallel chord truss)
[47] [钢结构][软件] 格构柱缀条布置方案力学概念测算对比 (Lace Bar Arrangement Patterns in Steel Lattice Column)
- 微信公众号 ( Wechat Subscription)


有意思的问题。简单计算的话,截面形心轴所在轴线处的轴向位移为零,支座截面底部出现向外轴向位移,位移值大约为梁端转角乘以形心高度。
的确是
期待更新 我也遇到类似问题不会计算
一般情况这个水平变形是很小的,基本可忽略,如果要从计算上去算,那有限元分析得考虑大变形几何非线性。