[数学][编程][混沌] 虫口模型的数值模拟 [Numerical simulation of insect population model]

实干、实践、积累、思考，创新。

---

1976 年 , 美国数学家梅 (May .R ) 在美国 《 自然 》 杂志上发表的题为 “ 具有复杂的动力学的简单模型 ” 文章中指出 , 在生态学中一些非常简单的确定性的数学模型却能产生看似随机的行为。如虫口模型：x_{n+ 1}= μx_n ( 1 -x _n )，其中 xn 是第n 年的虫口数，x_{n+ 1} 是第 n + 1 年的虫口数，x_n ∈ [0 , 1 ]，μ 为生殖增长率，取值范围为μ ∈ (0 , 4 )。固定参量 μ之后 , 取一个初值x₀代入 , 即可通过反复迭代，获得一系列的点x_i，其中每个 x _i (i = 1 , 2 , 3 ……)是一个轨道点，这样就得出一条轨道 。选择不同的参数 , 当迭代次数超过某个足够大的数 N 后 , 轨道会表现出一些奇特的行为 , 显示了虫口数随着时间推移的奇特变化情况 .

虫口模型实际为一个一维逻辑斯蒂映射Logistic map。（Link: Logistic模型）

虫口模型在混沌数学中是一个很经典的例子，它可以说明混沌可以从很简单的非线性方程中产生。

由于虫口模型就是一个简单的递推公式，可以非常简单的通过编程实现。

以下测试几个例子。

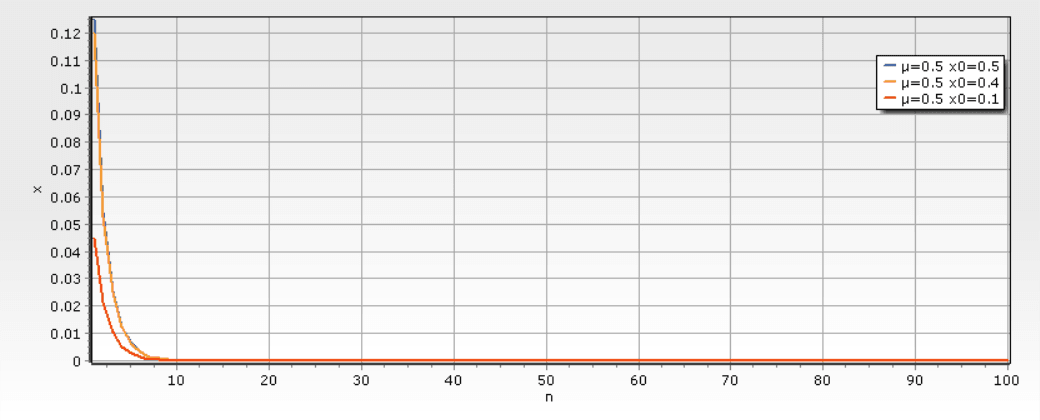
（1） μ= 0. 5，x₀分别取0.5、0.4及0.1可见，经过一定数量的迭代后，x_n趋于0，即种群趋于灭亡

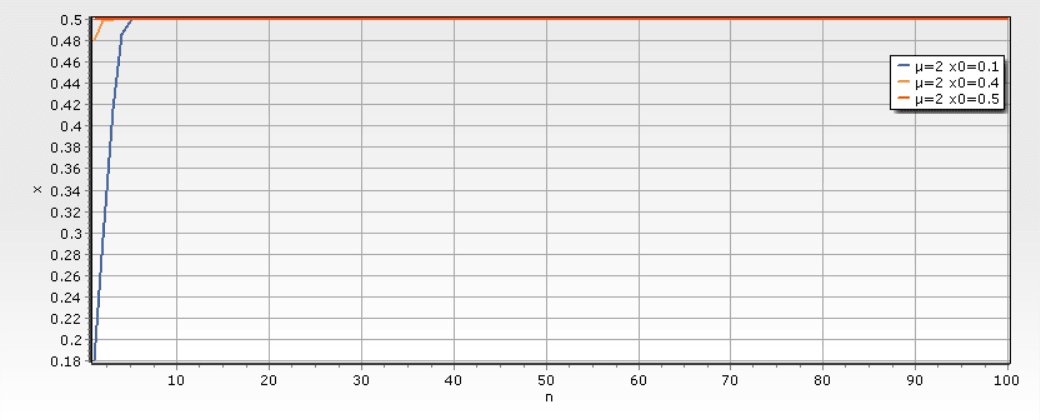
（2） μ= 2，x₀分别取0.5、0.4及0.1可见，经过一定数量的迭代后，x_n趋向于稳定的值0.5，即虫口数最终趋于同一个状态。

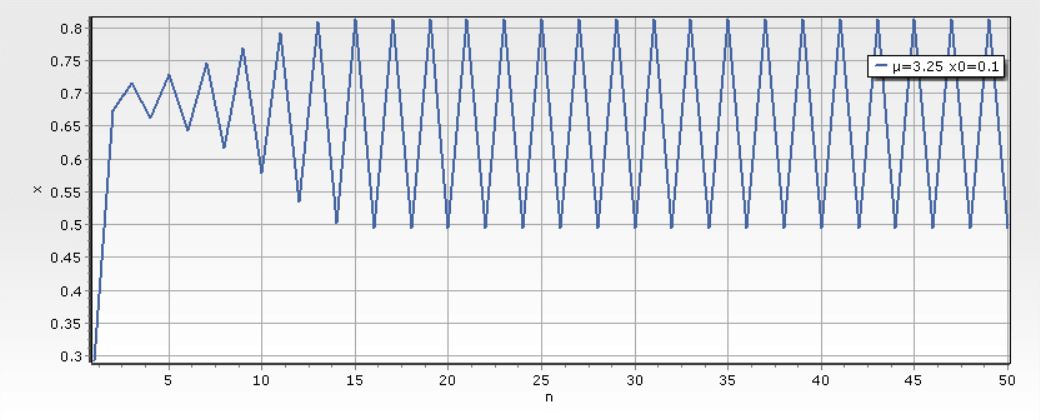
（3）随着μ的增大，随着参数 μ的继续增大，例如 μ= 3 . 25 时系统状态就会进入周期 2 轨道,系统出现两个值 x ∗1 和 x ∗2 的交替状态，即虫口数在两种状态之间交替变化。

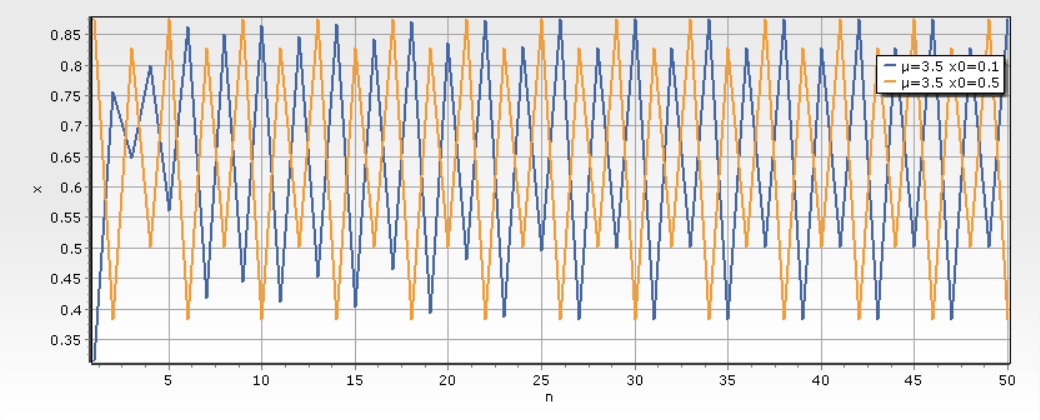
（4）如果进一步继续增加μ值，当 3 . 499 < μ ≤3 . 545 ,此时 x_n 在四个 值 上 依 次 跳 动.

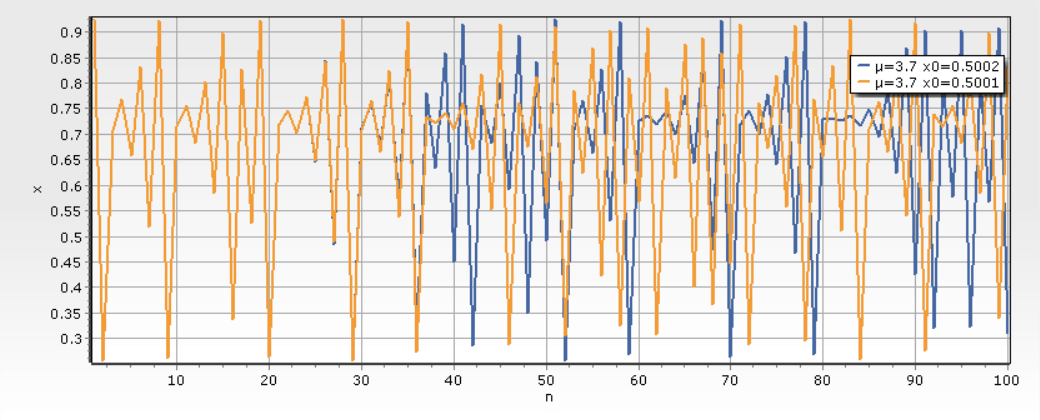
( 5 )继续增大参加μ的值，系统状态倍周期演化最终进入混沌轨道。例如取 μ= 3.7，初 值 分 别 为 x₀₁= 0.5001 和 x₀₂=0.5002。x₀₁与 x₀₂只有很小的差别 , 但我们可以明显的看到 , 迭 代 后的两条轨道最终表现出显著的差异。

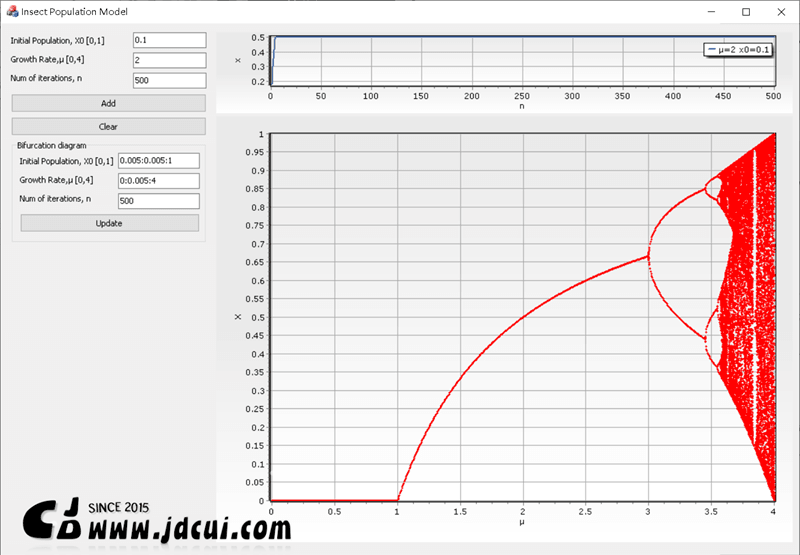
为了更全面的了解虫口方程演化过程，对μ及x₀取不同的值，绘制μ及x收敛值的分布图，即可得虫口模型的分岔图，如下：

• 相关博文 ( Related Topics)

[01] [编程][算法][几何] 编程训练: 凸包问题 [Convex-Hull Problem]

[02] [编程][算法][几何] 编程训练: 离散点的闭合路径 [Closed Path for points]

[03] [编程][算法][几何] 编程训练: 3次B样条曲线 [Cubic BSpline]

[04] [编程][算法][几何] 编程训练: 旅行商问题

[05] [编程][算法][几何] 编程训练: 3次Bezier曲线 [Cubic Bezier Curve]

[06] [编程][游戏][开发] 编程训练：数独游戏 ( Sudoku )

[07] [编程][软件][Programming] 编程训练：模拟退火算法(Simulated annealing algorithm)

[08] [编程][算法][优化] 编程训练：函数的CONLIN线性化

[09] [编程][算法][优化] 编程训练：函数的移动渐进线(MMA)近似

[09] [编程训练][Programming Training] URL Encode and Decode

[10] [游戏][编程][挑战] Programming challenge: Tetris Game [编程挑战: 俄罗斯方块游戏]

[11] [编程][软件][Tool] 幸运大抽奖程序 Lucky Draw

[12] Buffon’s Needle problem [蒲丰投针问题]

[13] [Game][游戏]CJD Core Ball[见缝插针游戏]

[14] Sierpinski Triangle by 1D Cellular Automata [1D元包自动机实现Sierpinski三角形]

[15] Cellular Automata Forest Fire Model [元包自动机森林火灾模型]

[16] Conway’s Game of Life [生命游戏]

[17] Mandelbrot Set & Julia Set [分形]

[18] Morley’s Theorem [莫利定理]

[19] Pascal’s Theorem [帕斯卡定理]

[20] [编程训练][Programming Training] Gaussian Distribution (高斯分布)

[21] [编程训练]Programming Training: Get Host

[22] [编程训练]Programming Training: Rotate Text

[23] [编程训练] 离散点的Delaunay三角形剖分( Delaunay triangulation of a point set)

[24] [编程训练] 图像分割 (Image segmentation)

[25] [编程训练] 拼图游戏 (Jigsaw Puzzle Game)

[26] [编程训练][Programming Training] Random number generator – Uniform Distribution (随机数生成器-均匀分布)

[27] [抽奖][软件][编程][年会] 2020公司年会抽奖 (图片抽奖) (RBS16周年纪念版) (Run by souls)

[28] [编程训练][游戏][数学] 红酒杯与白酒杯里到底有多少红酒和白酒？

[29] [数学][算法] 最小二乘法曲线拟合( Least square curve fitting )

[30] [编程][数学][编程训练] |x|^n+|y|^n=1小米logo轮廓曲线

[31] [数学][编程] 蒙特卡洛模拟法求圆周率π (Monte Carlo method to find PI)

[32] [编程训练] BMP图像缩放 (BMP Image scaling)

[33] [编程训练] 粒子群优化算法 [PSO: Particle Swarm Optimization]

[34] [编程][笔记] 如何将n^m个可能枚举出来？

[35] [数学][编程][混沌] 虫口模型的数值模拟 [Numerical simulation of insect population model]

---

• 微信公众号 ( Wechat Subscription)

欢迎关注 “结构之旅” 微信公众号