实干、实践、积累、思考、创新。
近日许多公众号分享了王亚勇大师提出的双向地震作用算法，许多群都进行了讨论。抱着好奇心，趁热打铁，这里也对这块内容做个测算研究。振型分解反应谱法，在计算双向地震作用时，涉及振型组合及方向组合。对于双向地震作用效应，我们是先振型组合，再方向组合？还是先方向组合，再振型组合？不同的组合顺序对结果有什么影响？以下通过算例做些探索。
1.1 测算目的
（1）了解振型分解反应谱法双向地震作用计算时，【先振型组合、再方向组合】与【先方向组合，再振型组合】的差异。先振型组合、再方向组合的结果大，还是先方向组合，再振型组合的结果大。
（2）测算王大师提出的双向地震作用计算方法与目前规范的双向地震作用计算方法的差异。这里贴一下王大师提出的算法的公式。原文见：
1.2 测算说明
（1）振型组合方式主要有SRSS方法、CQC方法和ABS法等。本文测算时，不管是【先振型组合、再方向组合】还是【先方向组合，再振型组合】，振型组合统一按CQC组合，这也是规范建议的方法。
（2）对于方向组合，考虑两种情况进行测算，分别是SRSS组合及ABS组合。对于SRSS及ABS组合，次方向的效应折减均取0.85。则，王大师建议的方法即，先方向组合，后振型组合，且方向组合采用ABS组合的方法。规范方法为，先振型租后，后方向组合，且方向组合采用SRSS组合的方法。
（3）测算的效应。由于王大师的ppt对新旧方法构件层次的内力响效应给出了较多例子。这里主要测算结构的宏观效应：楼层剪力及扭矩（累积扭矩）。结构的楼层剪力及累积扭矩值也是一种效应。
（4）测算的算法
假定，Sj(x)，Sj(y)分别为X向及Y向单向地震作用下振型分解反应谱法获得的结构的地震效效应。对于本文的测算，指的是结构的楼层剪力或累积扭矩。
A.对于先振型组合，后方向组合，方向组合采用SRSS组合的验算过程：
Step1：进行CQC振型组合，获得的两个方向地震作用振型组合后的效应S(x)及S(y)
其中，
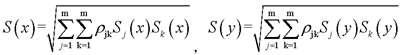
Step2: 进行SRSS方向组合，获得的X向为主方向及Y向为主方向的地震作用效应S(EX0.85EY)及S(EY0.85EX)。其中S(EX0.85EY) = sqrt( S(x)*S(x)+0.85*0.85*S(y)*S(y))
B.对于先方向组合，后振型组合，方向组合采用SRSS组合的验算过程：
Step1：先进行SRSS方向组合，X方向为主方向的地震效应为Sjmx =sqrt( Sj(x)*Sj(x)+0.85*0.85*Sj(y)*Sj(y))；Y方向为主方向的地震效应为Sjmy =sqrt(0.85*0.85* Sj(x)*Sj(x)+Sj(y)*Sj(y))
Step2：分别对Sjmx 及Sjmy 进行CQC振型组合，获得的X向为主方向及Y向为主方向的地震作用效应，同样命名为S(EX0.85EY)及S(EY0.85EX)，其中，
，
C.对于先振型组合，后方向组合，方向组合采用ABS组合的验算过程：
Step1：进行CQC振型组合，获得的两个方向地震作用振型组合后的效应S(x)及S(y)
其中，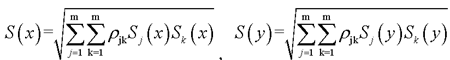
，
Step2: 进行ABS方向组合，获得的X向为主方向及Y向为主方向的双向地震作用效应S(EX0.85EY)及S(EY0.85EX)。其中S(EX0.85EY) = S(x)+0.85*S(y)，S(EY0.85EX)=0.85* S(x)+S(y).
- 对于先方向组合，后振型组合，方向组合采用ABS组合（王大师提取的新算法）的验算过程：
Step1：进行ABS方向组合，根据王大师的提出的新算法，基于作用组合，考虑0.85倍次方向地震作用正负，由于是弹性系统，且是线性作用组合，所以，相当于效应考虑0.85倍次方向的效应正负做组合。为此一共考虑4个效应组合。
Sj1(x) = Sj(x)+0.85Sj(y) ; Sj2(x) = Sj(x)-0.85Sj(y) ;
Sj3(x) = Sj(y)+0.85Sj(x) ; Sj4(x) = Sj(y)-0.85Sj(x) ;
其中，Sj1(x) , Sj2(x) 可以认为是X向为主向的双向地震下的效应; Sj3(x) , Sj4(x) 是Y向为主向的双向地震下的效应；
Step2：对4个公开均进行CQC组合，获得Si，
其中，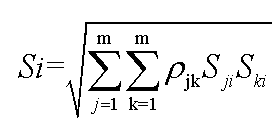
，i分别取1，2，3，4。
则，S1及S2取包络为X向为主方向的双向地震作用效应，即S(EX0.85EY)=max( S1,S2)，对S3及S4取包络为Y向为主方向的双向地震作用效应，即S(EY0.85EX))=max( S1,S2)。
1.3 案例测算
有了前面的算法，采用YJK程序对几个案例进行反应谱分析，并通过编制程序对YJK的振型分解反应谱结果进行二次处理，即可获得案例不同组合方法的计算结果。二次开发的软件界面如下：
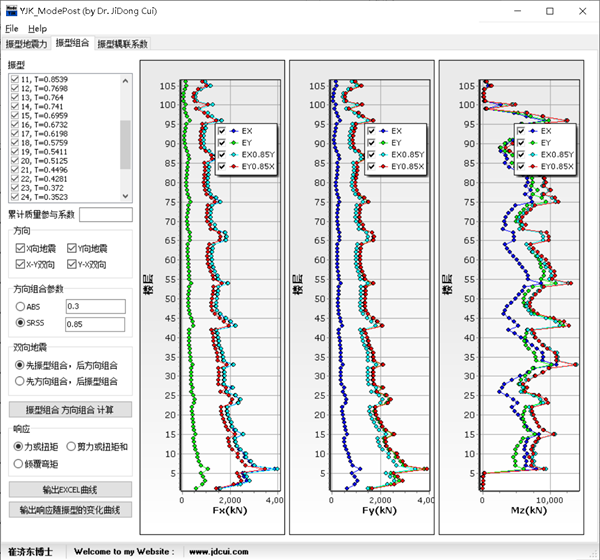
此外，后续结果中，Vx表示结构X方向的层地震剪力，Vy表示结构Y方向的层地震剪力，Mzt表示结构绕Z轴的楼层扭矩。
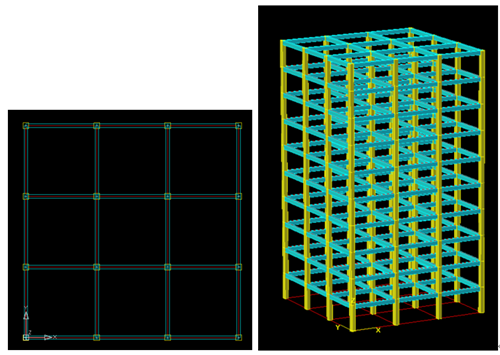
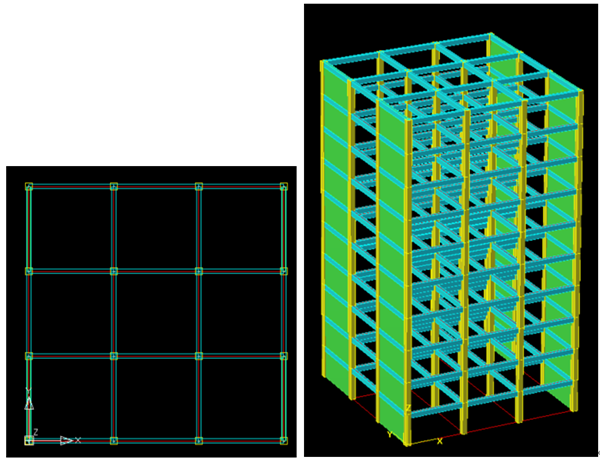
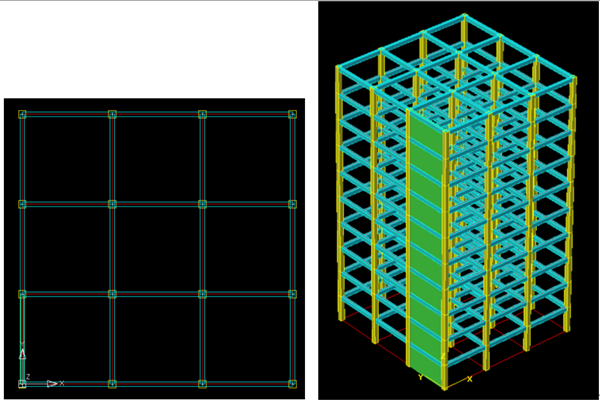
1.3.1 案例1（10层3X3跨刚度双向对称框架结构）
10层，3X3跨的框架结构，X 、Y向刚度对称。结构特点是：（1）平动与扭转不耦联，即平动振型不包含扭转成分，反之亦然。（2）X向与Y向平动振型耦联较少。
（1）方向组合为SRSS的测算结果：
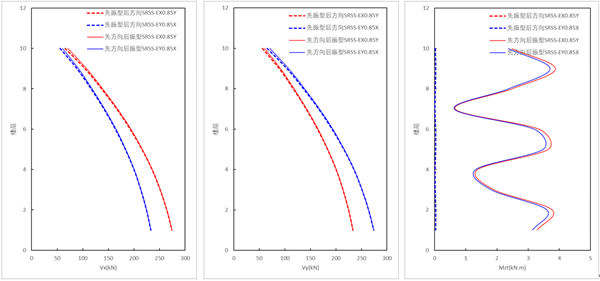
由上图可知，采用SRSS方向组合时，【先振型组合，后方向组合（规范法）】的结果 小于 【先方向组合，后振型组合的结果】，剪力相差不大（仅在在塔楼顶部出现差异，主要是高阶振型的影响，高阶平动振型之间存在耦联），扭矩相差较大。
（2）方向组合为ABS的测算结果：
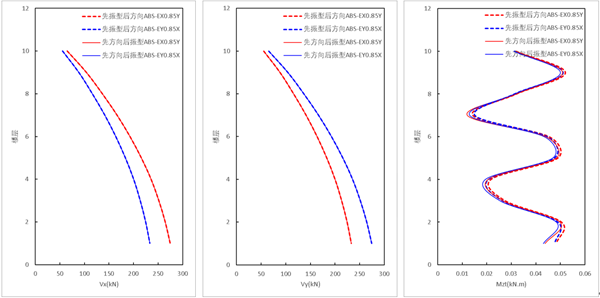
由上图可知，采用ABS方向组合时，先振型组合，后方向组合的结果 大于 先方向组合，后振型组合（新方法）的结果，对于该模型剪力及扭矩均相差不大。
（3）规范法与新方法的差异对比：
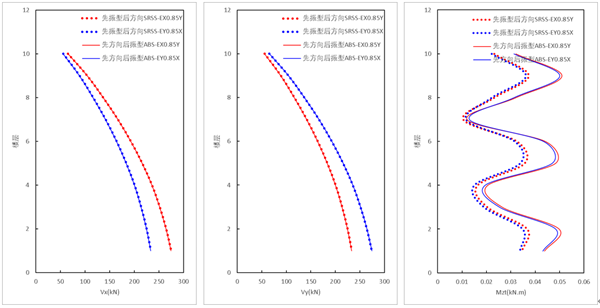
新方法（ABS方向组合,先方向组合,后振型组合）的剪力结果与规范法结果一致；但新方法的扭矩结果比规范法结果大（该模型扭矩绝对值较小）。
1.3.2 案例2（10层3X3跨，XY向刚度不等，框架结构）
10层，3X3跨的框架结构，X 、Y向刚度差别大。结构特点是：（1）平动振型与扭转振型不耦联，即平动振型不包含扭转成分。（2）X向平动振型与Y向平动振型无耦联（案例1的更近一步）。即3个方向的振型均不耦联。
（1）方向组合为SRSS的测算结果
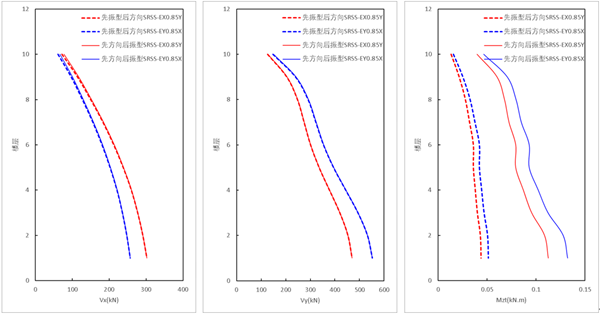
由上图可知，采用SRSS方向组合时，【先振型组合，后方向组合（规范法）】的结果 小于 【先方向组合，后振型组合的结果】，剪力基本无差异，扭矩相差较大。
（2）方向组合为ABS的测算结果
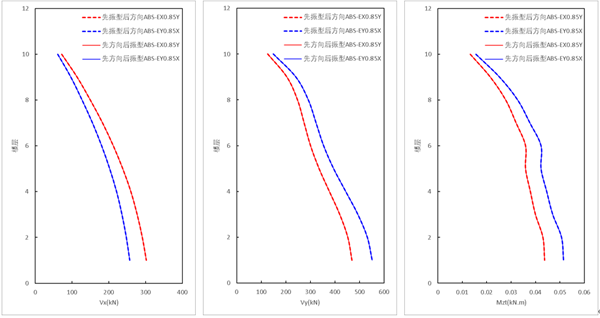
由上图可知，对于该模型，采用ABS方向组合时，【先振型组合，后方向组合（规范法）】的结果 与 【先方向组合，后振型组合的结果】一致。即当，模型各振型均仅含某个方向的变形时(即某单向水平地震作用下，最多仅引起各振型该方向的地震力)，双向地震组合方向组合采用ABS方法的计算结果与组合顺序无关。
（3）规范法与新方法的差异对比
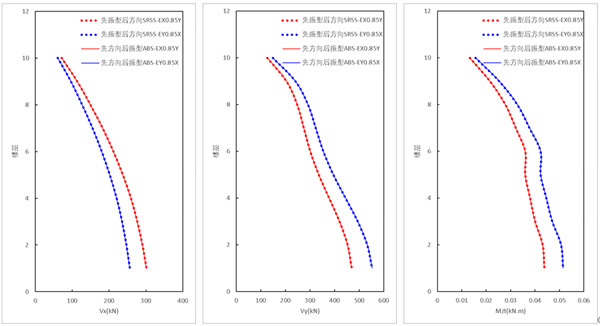
新方法（ABS方向组合,先方向组合,后振型组合）的剪力结果与规范法结果一致。
1.3.3 案例3（10层3X3跨，XY向刚度不等，框架结构）
10层，3X3跨的框架结构，刚度偏心。结构特点是：（1）平动与扭转耦联。（2）X向平动与Y向平动也耦联。
（1）方向组合为SRSS的测算结果
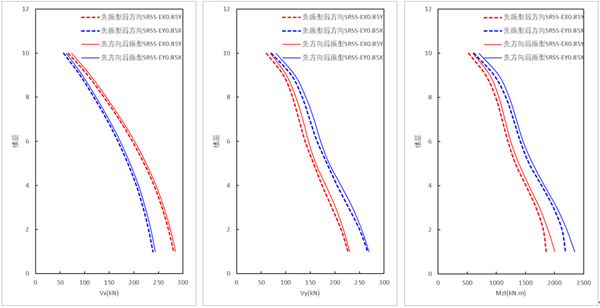
采用SRSS方向组合时，【先振型组合，后方向组合（规范法）】的结果 小于 【先方向组合，后振型组合的结果】。
（2）方向组合为ABS的测算结果
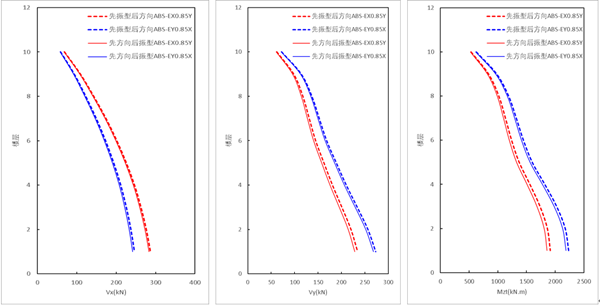
采用ABS方向组合时，【先振型组合，后方向组合】的结果 大于 【先方向组合，后振型组合（新方法）】的结果，对于该模型剪力及扭矩均相差不大。
（3）规范法与新方法的差异对比
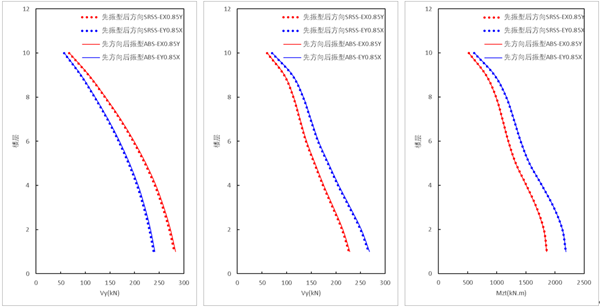
新方法（ABS方向组合,先方向组合,后振型组合）的剪力结果略大于规范法结果，两种方法扭矩结果一致。
1.3.4 案例4（实际工程：12层框剪结构）
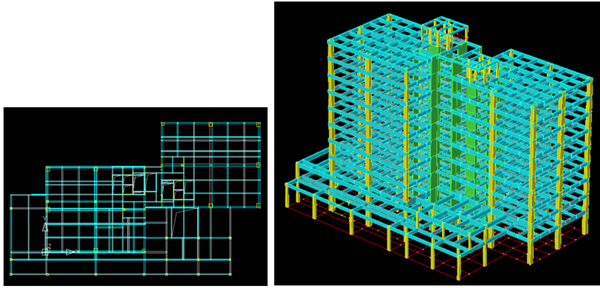
- 方向组合为SRSS的测算结果
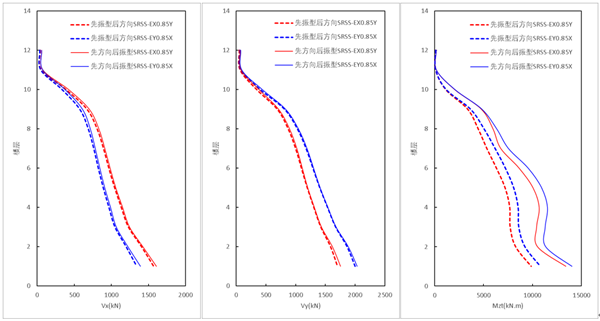
采用SRSS方向组合时，【先振型组合，后方向组合（规范法）】的结果 小于 【先方向组合，后振型组合的结果】，其中剪力相差不大，但先方向组合的扭矩结果增加较大。
- 方向组合为ABS的测算结果
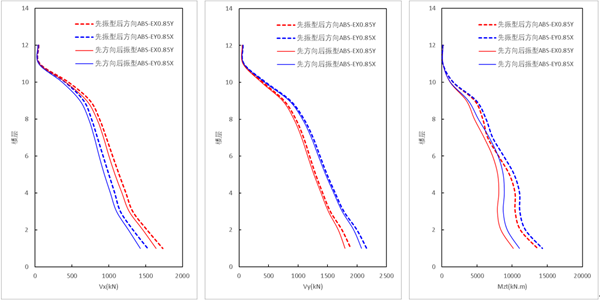
采用ABS方向组合时，【先振型组合，后方向组合】的结果 大于 【先方向组合，后振型组合（新方法）】的结果，其中基底剪力大2%，基底扭矩大4%。
（3）规范法与新方法的差异对比
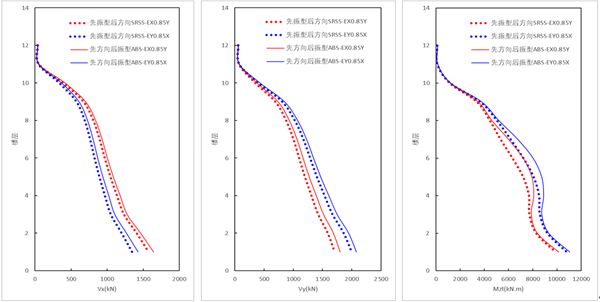
新方法（ABS方向组合,先方向组合,后振型组合）的结果略大于规范法结果，基底响应结果增大比例在2%~4%，其中，可以发现，新方法在楼层中部的扭矩较规范法的扭矩增大程度比其余楼层范围大。
1. 案例5（实际工程：48层框剪结构）
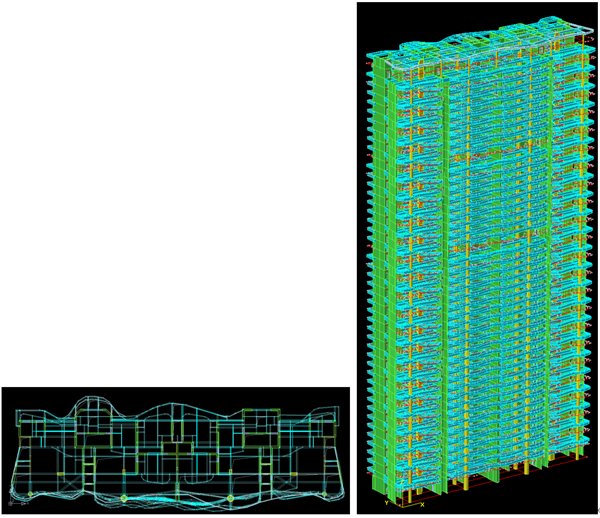
- 方向组合为SRSS的测算结果
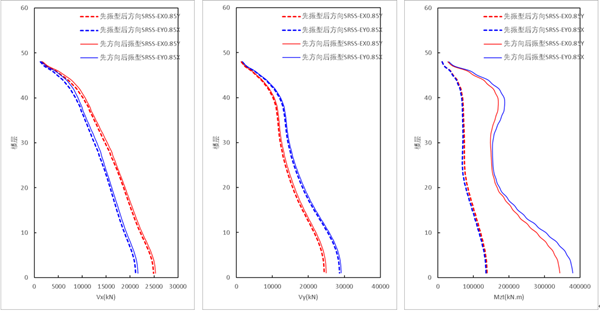
采用SRSS方向组合时，【先方向组合，后振型组合的结果】大于【先振型组合，后方向组合（规范法）】的结果，其中剪力相差不大，扭矩差距较大。其中，【先方向组合，后振型组合的结果】的扭矩大于【先振型组合，后方向组合（规范法）】结果的两倍。
- 方向组合为ABS的测算结果
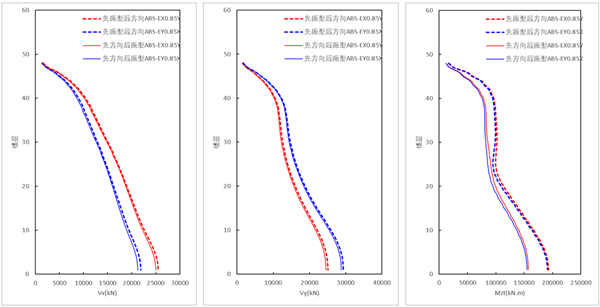
采用ABS方向组合时，【先振型组合，后方向组合】的结果 大于 【先方向组合，后振型组合（新方法）】的结果，扭矩增大的幅度比剪力增大的幅度大。
（3）规范法与新方法的差异对比
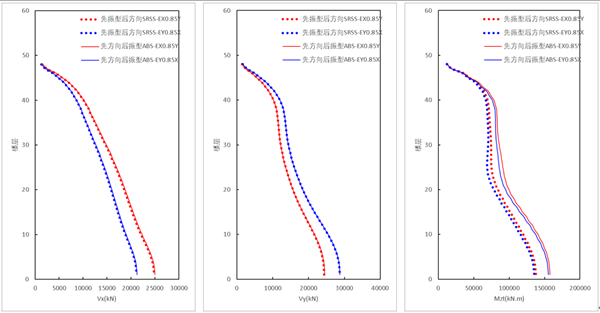
新方法（ABS方向组合,先方向组合,后振型组合）的结果大于规范结果，其中新方法基底剪力略大于规范法结果，新方法扭矩比规范法的扭矩增大15%。
案例6（实际工程修改：48层框筒结构）
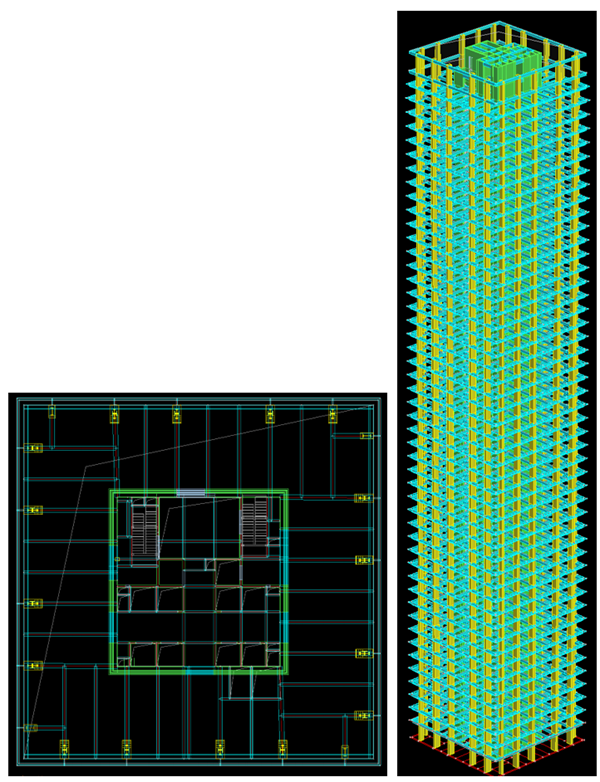
（1）方向组合为SRSS的测算结果
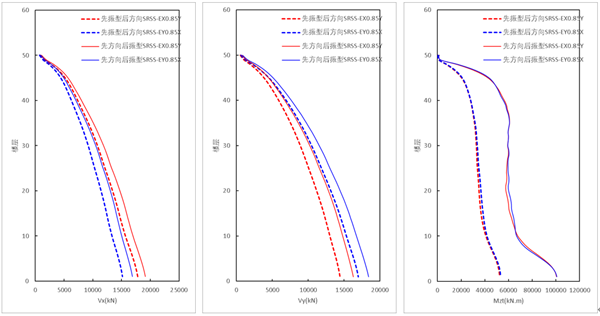
采用SRSS方向组合时，【先振型组合，后方向组合（规范法）】的结果 小于 【先方向组合，后振型组合的结果】，对于该模型，【先方向组合】的剪力大概为【先振型组合】结果的1.07，扭矩结果的这一比值约为1.9倍。
（2）方向组合为ABS的测算结果
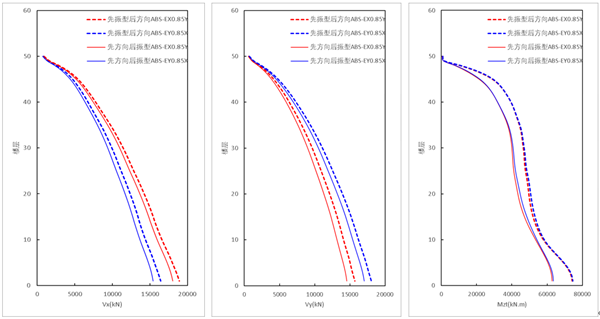
采用ABS方向组合时，【先振型组合，后方向组合（规范法）】的结果 大于 【先方向组合，后振型组合的结果】，其中剪力增大幅度较小，扭矩增加的幅度大于剪力增加的幅度。
（3）规范法与新方法的差异对比
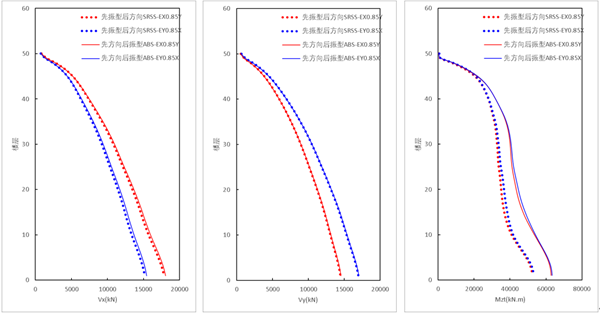
新方法（ABS方向组合,先方向组合,后振型组合）的结果大于规范法结果，其中剪力结果基本一致，新方法扭矩相比规范法，增大约10%。
案例7（实际工程：某500m超高层结构，结构体系为RC核心筒+巨柱+伸臂+巨型斜撑）
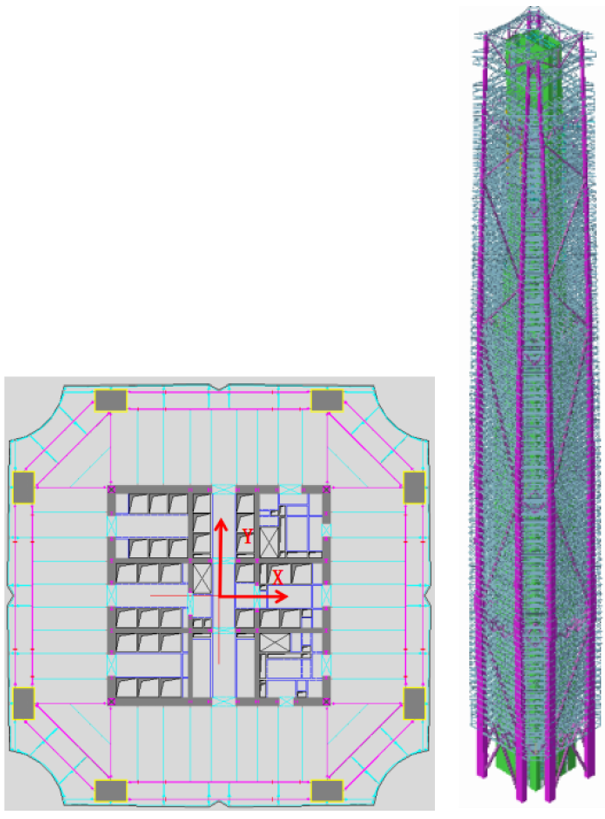
- 方向组合为SRSS的测算结果
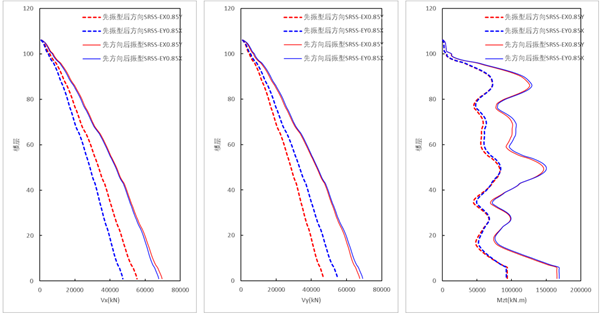
采用SRSS方向组合时，【先方向组合，后振型组合的结果】大于【先振型组合，后方向组合（规范法）】的结果，其中基底剪力增大越25%，扭矩增大约80%。
- 方向组合为ABS的测算结果
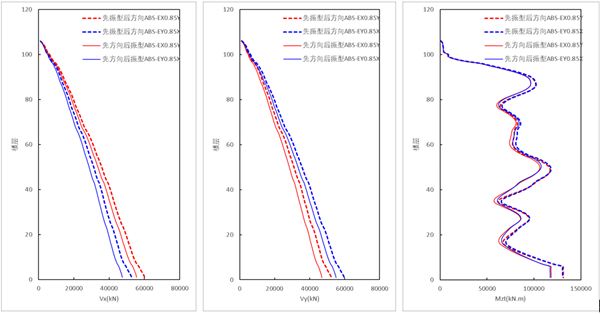
采用ABS方向组合时，【先方向组合，后振型组合的结果】小于【先振型组合，后方向组合（规范法）】的结果，其中基底剪力增大越25%，扭矩增大约80%。
（3）规范法与新方法的差异对比
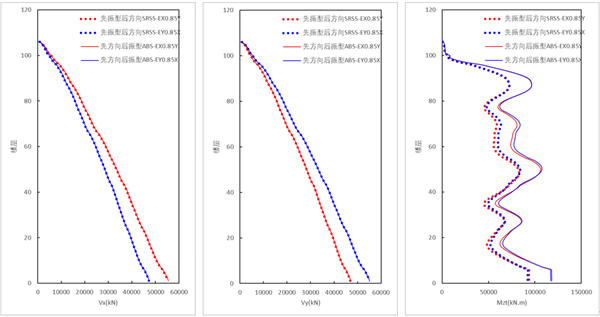
新方法（ABS方向组合,先方向组合,后振型组合）的剪力结果与规范法结果基本一致，新方法的扭矩结果大于规范法结果，增大比例在25%。
1.4 小结
由以上分析，似乎可以大致得到以下结论（以下结论均是基于双向地震效应（对于本文，主要指剪力及扭矩）、且不管方向组合选SRSS法还是ABS法，次方向的折减系数均为0.85的前提条件）：
（1）振型组合采用CQC组合，方向组合采用SRSS组合时，【先振型组合，后方向组合（规范法）】的结果不大于【先方向组合，后振型组合的结果】。
（2）振型组合采用CQC组合，方向组合采用ABS组合时，【先振型组合，后方向组合（规范法）】的结果不小于【先方向组合，后振型组合的结果】。与方向组合采用SRSS法时相反。
（3）选用同一种方向组合方法的情况下，对于因振型组合与方向组合次序引起的结果的增大或减小的剧烈程度而言，方向组合采用SRSS比采用ABS剧烈。这点也好理解，简单说就是非线性操作（SRSS比平方和开根号）线性操作（ABS）激烈。
（4）选用同一种方向组合方法的情况下，振型组合与方向组合次序引起的剪力的增大或减小的剧烈程度小于扭矩的。这点似乎也可以解释，对于双向地震，某种意义上来说，是地震的斜向输入，对于双向地震的两个主方向的剪力，可以理解为斜向地震剪力沿两个方向的分解，对于扭矩，则不存在斜向分解一说，两个方向地震作用产生的扭矩是直接叠加的，会增加更多。对应到构件层次，就是构件剪力与构件轴力的关系，可能双向地震对于构件剪力放大不明显，但是对于轴力可能就放大很多。这也是为何对于扭矩不规则结果，我们要用考虑双向地震及扭转不规则的原因。
（5）新方法（ABS方向组合,先方向组合,后振型组合）的结果不小于规范法（SRSS方向组合，先振型组合，后方向组合）结果。
（6）对于测算的几个实际工程案例（工程案例均来源于RBS），案例4采用新方法获得的效应比规范法获得效应增大在2~4%，其余结构，新方法的结构基底剪力与规范法剪力均差别不大，新方法结构基底扭矩比规范法结果增大10~25%不等。
（7）文中对比的是结构的整体效应（剪力、扭矩），由于组合过程的非线性，不同组合方法或组合顺序引起的整体响应增大或者减小的程度的大小与对应的构件效应（构件剪力、弯矩、轴力等）增大或减小的程度的大小是不同的。
1.5 参考
[1] 建筑结构丨王亚勇大师：浅谈双向地震作用和地震效应组合（https://mp.weixin.qq.com/s/zFPDNxsuGQAzq0wkWRLWFQ） [2] 结构微学堂 | 对于双向地震作用效应，我们是先振型组合，再方向组合？还是先方向组合，再振型组合？( https://mp.weixin.qq.com/s/rZjICNxqd7Gm-ekg7ndTYg )
- 微信公众号 ( Wechat Subscription)
欢迎关注 “结构之旅” 微信公众号
