实干、实践、积累、思考、创新。
接着博文《[力学][有限元][FEM]Basics of Buckling Analysis [曲屈分析基础]》继续介绍经典材料力学或结构力学课本上介绍的压杆稳定问题。该部分内容也是 书本 《有限单元法:编程与软件应用》屈曲分析章节的部分内容节选。
11.5 屈曲分析3:压杆稳定
作为屈曲分析的补充,本节讨论一下压杆稳定问题。
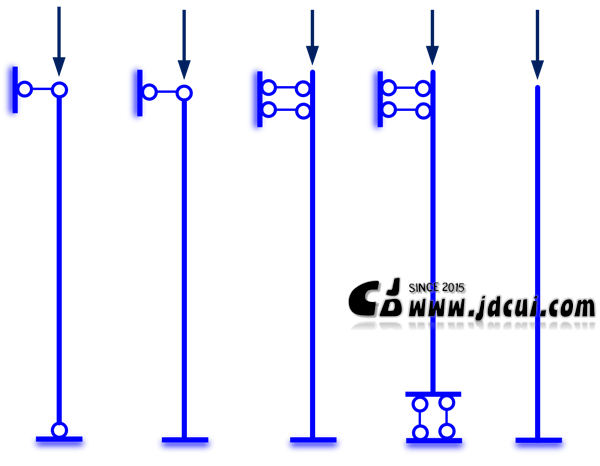
图 11‑10 压杆支座情况
算例结构为一根等截面轴心受压直杆,直杆材料为钢管,钢管外径100mm,管厚5mm,高5m。一共考虑了5种约束情况,分别为:1.两端铰接;2.一端铰接、一端嵌固;3.两端嵌固;4.一端嵌固、一端滑动;5.一端嵌固、一端自由。针对每种约束情况,分别将压杆划分为1个、2个、5个、10个、20个梁单元,进行屈曲分析。
11.5.1 MATLAB代码与注释
本节以底端嵌固、上端自由、划分20个单元的情况为例,给出进行屈曲分析所需的主要代码。
% Pressed Bar Buckling Analysis
% Author : JiDong Cui(崔济东),Xuelong Shen(沈雪龙)
% Website : www.jdcui.com
% 20170609
注释:代码说明。
% Clear all parameters
clear all
clc
注释:删除MATLAB工作空间中的所有变量,并释放系统内存。“clc”的作用是清除命令行的历史文件。
% Format of data output
format shortEng
注释:该段代码对数据输出显示格式进行设置,指定格式为“shortEng”,在该格式下,结果数据以工程计数法的形式输出,即将数字表示成10的幂的倍数,且将10的幂限制为3的倍数,如a×103i,i为整数。
% Properties definition
E = 2.0E+05;
A = 1492.2565;
I = 1688115.2;
注释:该段代码定义了若干变量,包括材料的弹性模量E、截面面积A和截面惯性矩 I。
% Node coordinates
nodeCoord = [0 0;0 250;0 500;0 750;0 1000;0 1250;0 1500;0 1750;0 2000;0 2250;0 2500;0 2750;0 3000;0 3250;0 3500;0 3750;0 4000;0 4250;0 4500;0 4750;0 5000];
注释:本算例只进行XY平面内分析,压杆分为20个单元,一共有21个节点,每个节点有x、y两个坐标,因此该段代码定义了一个21×2矩阵NodeCoord,用于存储结构中21个节点的x、y坐标。
% Element nodes
EleNode = [1 2;2 3;3 4;4 5;5 6;6 7;7 8;8 9;9 10;10 11;11 12;12 13;13 14;14 15;15 16;16 17;17 18;18 19;19 20;20 21];
注释:本算例共有20个单元,每个单元有2个节点,因此该段代码定义了一个20×2的矩阵EleNode,用于存储20个单元的节点编号。
restrainedDof = [1 2 3];
注释:本算例中,节点1的x平动、y平动、绕z转动自由度被约束,对应的整体自由度的编号分别是1、2、3,因此该段代码定义了一个1×3的行向量restrainedDof,用于存储约束自由度编号。
% Number of elements and nodes
numEle = size(EleNode,1)
numNode = size(nodeCoord,1)
注释:该段代码定义了两个变量numEle和numNode,分别用于存储结构中的单元数量(即矩阵EleNode的行数)和节点数量(即矩阵NodeCoord的行数)。本例中numEle=20,numNode=21。
% X coordination and Y coordination of all nodes
xx = nodeCoord(:,1)
yy = nodeCoord(:,2)
注释:该段代码定义了两个21×1的列向量xx和yy,分别用于存储所有节点的x坐标和所有节点的y坐标。
% Total number of freedom
numDOF = numNode*3;
注释:该段代码定义了一个变量numDOF,用于存储自由度的总数。本算例共有21个节点(numNode=21),每个节点有3个自由度,因此numDOF的值为21×3=63。
% Loading
force(62)=-1; %20 element
注释:本算例在节点21处施加了-z方向的单位集中力,节点21的-z方向平动自由度对应整体自由度的编号为62,因此该段代码为整体节点力向量force的相应元素赋值,指定force(62)的值为-1,其余元素的值仍为0。
% Global stiffness matrix
stiffness = zeros(numDOF);
for i=1:numEle;
noindex = EleNode(i,:);
deltax = xx( noindex(2)) - xx( noindex(1));
deltay = yy( noindex(2)) - yy( noindex(1));
L = sqrt( deltax*deltax + deltay*deltay );
C = deltax / L;
S = deltay / L;
% Element stiffness matrix
T = [ C S 0 0 0 0;
-S C 0 0 0 0;
0 0 -1 0 0 0;
0 0 0 C S 0;
0 0 0 -S C 0;
0 0 0 0 0 -1
];
EAL = E*A/L;
EIL1 = E*I/L;
EIL2 = 6.0*E*I/(L*L);
EIL3 = 12.0*E*I/(L*L*L);
eleK = [ EAL 0 0 -EAL 0 0;
0 EIL3 EIL2 0 -EIL3 EIL2;
0 EIL2 4*EIL1 0 -EIL2 2*EIL1;
-EAL 0 0 EAL 0 0;
0 -EIL3 -EIL2 0 EIL3 -EIL2;
0 EIL2 2*EIL1 0 -EIL2 4*EIL1
];
eleDof = [noindex(1)*3-2 noindex(1)*3-1 noindex(1)*3 noindex(2)*3-2 noindex(2)*3-1 noindex(2)*3];
% Integrate element stiffness matrix to the global stiffness matrix
stiffness( eleDof , eleDof) = stiffness( eleDof,eleDof) + T'*eleK*T;
end
% Unrestrained freedom
activeDof = setdiff( [1:numDOF]',restrainedDof);
% Solute balance function
disp('Displacement');
displacement(activeDof) = stiffness( activeDof , activeDof)\force(activeDof);
注释:上述代码建立平衡方程并求解。
% Element axial force
AxialForce=zeros(numEle,1);
for i=1:numEle
noindex = EleNode(i,:);
deltax = xx( noindex(2)) - xx( noindex(1));
deltay = yy( noindex(2)) - yy( noindex(1));
L = sqrt( deltax*deltax + deltay*deltay );
% Element stiffness matrix
C = deltax / L;
S = deltay / L;
T = [ C S 0 0 0 0;
-S C 0 0 0 0;
0 0 1 0 0 0;
0 0 0 C S 0;
0 0 0 -S C 0;
0 0 0 0 0 1
];
EAL = E*A/L;
EIL1 = E*I/L;
EIL2 = 6.0*E*I/(L*L);
EIL3 = 12.0*E*I/(L*L*L);
eleK = [ EAL 0 0 -EAL 0 0;
0 EIL3 EIL2 0 -EIL3 EIL2;
0 EIL2 4*EIL1 0 -EIL2 2*EIL1;
-EAL 0 0 EAL 0 0;
0 -EIL3 -EIL2 0 EIL3 -EIL2;
0 EIL2 2*EIL1 0 -EIL2 4*EIL1
];
eleDof = [noindex(1)*3-2 noindex(1)*3-1 noindex(1)*3 noindex(2)*3-2 noindex(2)*3-1 noindex(2)*3];
ue=displacement(eleDof,:);
uep=T*ue;
fp=eleK*uep;
AxialForce(i)=fp(4);
end
注释:上述代码用于求解各个单元的轴力,存放在数组AxialForce中,用于后续求解单元几何刚度矩阵。
% Geometric Stiffness Matrix
stiffnessM = zeros(numDOF);
stiffnessG = zeros(numDOF);
for i=1:numEle;
noindex = EleNode(i,:);
deltax = xx( noindex(2)) - xx( noindex(1));
deltay = yy( noindex(2)) - yy( noindex(1));
L = sqrt( deltax*deltax + deltay*deltay );
C = deltax / L;
S = deltay / L;
T = [ C S 0 0 0 0;
-S C 0 0 0 0;
0 0 -1 0 0 0;
0 0 0 C S 0;
0 0 0 -S C 0;
0 0 0 0 0 -1
];
EAL = E*A/L;
EIL1 = E*I/L;
EIL2 = 6.0*E*I/(L*L);
EIL3 = 12.0*E*I/(L*L*L);
eleKm = [ EAL 0 0 -EAL 0 0;
0 EIL3 EIL2 0 -EIL3 EIL2;
0 EIL2 4*EIL1 0 -EIL2 2*EIL1;
-EAL 0 0 EAL 0 0;
0 -EIL3 -EIL2 0 EIL3 -EIL2;
0 EIL2 2*EIL1 0 -EIL2 4*EIL1
];
eleKgu=AxialForce(i)/L*[0, 0, 0,0, 0, 0;
0, 6/5, L/10,0, -6/5, L/10;
0,L/10,2*L^2/15,0,-L/10, -L^2/30;
0, 0, 0,0, 0, 0;
0,-6/5, -L/10,0, 6/5, -L/10;
0,L/10, -L^2/30,0,-L/10,2*L^2/15
];
eleKg=T'*eleKgu*T;
eleDof = [noindex(1)*3-2 noindex(1)*3-1 noindex(1)*3 noindex(2)*3-2 noindex(2)*3-1 noindex(2)*3];
stiffnessM( eleDof , eleDof) = stiffnessM( eleDof,eleDof) + T'*eleKm*T;
stiffnessG( eleDof , eleDof) = stiffnessG( eleDof , eleDof) + eleKg;
end
注释:本段代码主要用于根据单元几何刚度矩阵和单元内力求得结构整体几何刚度矩阵。
% Solution
A=-stiffnessM(activeDof,activeDof)\stiffnessG(activeDof,activeDof);
[Vo,Do] = eig(A); % Get the eigenvalues and eigenvectors
fo=diag(Do);
Vf=sortrows([Vo',fo],size(Vo,1)+1);
V=Vf(:,1:size(Vo,1))';
f=sort(fo);
fac=1./f
fac=1./f
本段代码通过求解标准特征值问题,求得特征值和特征向量。Matlab内置函数 eig([A]) 可直接求解特征值和特征向量,求得的特征值放在向量 {Do} 中,相应的特征向量放在矩阵 [Vo] 中。其后的代码用于处理求解得到的数据,其中代码“V=”用于将特征向量排序,代码“f=”用于将结构自振频率进行排序,代码 “fac=” 用于求得屈曲因子,即特征值的倒数。图 11‑3所示是该桁架结构的前三阶屈曲模态。
11.5.2 SAP2000分析
由于压杆模型较为简单,此处不再赘述建模过程。需要注意的是,这里在压杆顶端施加的荷载为1,如此算出来的屈曲因子也就等于压杆的临界承载力。
各约束情况下压杆临界承载力的MATLAB分析结果与SAP2000分析结果及其与理论解的对比列表如下。
表 11‑3 约束情况1:两端铰接(单位:N)
| 约束情况 | 两端铰接 | ||||
| 单元划分 | 理论解 | SAP2000 | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 133288 | 162059 | 21.585 | 162059 | 21.585 |
| 2 | 133288 | 134290 | 0.752 | 134291 | 0.752 |
| 5 | 133288 | 133317 | 0.022 | 133317 | 0.022 |
| 10 | 133288 | 133290 | 0.001 | 133290 | 0.001 |
| 20 | 133288 | 133288 | 0.000 | 133288 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=133288N,其中μ=1.0。
表 11‑4 约束情况2:一端铰接、一端固定(单位:N)
| 约束情况 | 一端铰接一端固定 | ||||
| 单元划分 | 理论解 | SAP2000 | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 266657 | 405148 | 51.936 | 405148 | 51.936 |
| 2 | 266657 | 279671 | 4.880 | 279671 | 4.880 |
| 5 | 266657 | 272910 | 2.345 | 272910 | 2.345 |
| 10 | 266657 | 272689 | 2.262 | 272690 | 2.262 |
| 20 | 266657 | 272675 | 2.257 | 272675 | 2.257 |
注:压杆临界承载力理论值:π2EI/(μl)2=266657N,其中μ=0.707。
表 11‑5 约束情况3:两端嵌固(单位:N)
| 约束情况 | 两端嵌固 | ||||
| 单元划分 | 理论解 | SAP2000 | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 533153 | – | – | – | – |
| 2 | 533153 | 540197 | 1.321 | 540197 | 1.321 |
| 5 | 533153 | 534862 | 0.321 | 534862 | 0.321 |
| 10 | 533153 | 533266 | 0.021 | 533266 | 0.021 |
| 20 | 533153 | 533160 | 0.001 | 533160 | 0.001 |
注:压杆临界承载力理论值:π2EI/(μl)2=533153N,其中μ=0.5。
表 11‑6 约束情况4:一端嵌固、一端滑动(单位:N)
| 约束情况 | 一端嵌固、一端滑动 | ||||
| 单元划分 | 理论解 | SAP2000 | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 133288 | 135049 | 1.321 | 135049 | 1.321 |
| 2 | 133288 | 134291 | 0.752 | 134291 | 0.752 |
| 5 | 133288 | 133317 | 0.022 | 133317 | 0.022 |
| 10 | 133288 | 133290 | 0.001 | 133290 | 0.001 |
| 20 | 133288 | 133288 | 0.000 | 133288 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=133288N,其中μ=1.0。
表 11‑7 :约束情况5:一端嵌固、一端自由(单位:N)
| 约束情况 | 一端嵌固、一端自由 | ||||
| 单元划分 | 理论解 | SAP2000 | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 33322 | 33573 | 0.753 | 33573 | 0.753 |
| 2 | 33322 | 33339 | 0.051 | 33339 | 0.051 |
| 5 | 33322 | 33323 | 0.003 | 33323 | 0.003 |
| 10 | 33322 | 33322 | 0.000 | 33322 | 0.000 |
| 20 | 33322 | 33322 | 0.000 | 33322 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=33322N,其中μ=2.0。
11.5.3 midas Gen分析
压杆模型的midas Gen建模思路与SAP2000类似,此处不再赘述。
各约束情况下压杆临界承载力的MATLAB分析结果与midas Gen分析结果及其与理论解的对比列表如下。
表 11‑8 约束情况1:两端铰接(单位:N)
| 约束情况 | 两端铰接 | ||||
| 单元划分 | 理论解 | midas Gen | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 133288 | 162059 | 21.585 | 162059 | 21.585 |
| 2 | 133288 | 134290 | 0.752 | 134291 | 0.752 |
| 5 | 133288 | 133317 | 0.022 | 133317 | 0.022 |
| 10 | 133288 | 133290 | 0.001 | 133290 | 0.001 |
| 20 | 133288 | 133288 | 0.000 | 133288 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=133288N,其中μ=1.0。
表 11‑9 约束情况2:一端铰接、一端固定(单位:N)
| 约束情况 | 一端铰接一端固定 | ||||
| 单元划分 | 理论解 | midas Gen | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 266657 | 405148 | 51.936 | 405148 | 51.936 |
| 2 | 266657 | 279671 | 4.880 | 279671 | 4.880 |
| 5 | 266657 | 272910 | 2.345 | 272910 | 2.345 |
| 10 | 266657 | 272689 | 2.262 | 272690 | 2.262 |
| 20 | 266657 | 272675 | 2.257 | 272675 | 2.257 |
注:压杆临界承载力理论值:π2EI/(μl)2=266657N,其中μ=0.707。
表 11‑10 约束情况3:两端嵌固(单位:N)
| 约束情况 | 两端嵌固 | ||||
| 单元划分 | 理论解 | midas Gen | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 533153 | – | – | – | – |
| 2 | 533153 | 540197 | 1.321 | 540197 | 1.321 |
| 5 | 533153 | 534862 | 0.321 | 534862 | 0.321 |
| 10 | 533153 | 533266 | 0.021 | 533266 | 0.021 |
| 20 | 533153 | 533160 | 0.001 | 533160 | 0.001 |
注:压杆临界承载力理论值:π2EI/(μl)2=533153N,其中μ=0.5。
表 11‑11 约束情况4:一端嵌固、一端滑动(单位:N)
| 约束情况 | 一端嵌固、一端滑动 | ||||
| 单元划分 | 理论解 | midas Gen | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 133288 | 135049 | 1.321 | 135049 | 1.321 |
| 2 | 133288 | 134291 | 0.752 | 134291 | 0.752 |
| 5 | 133288 | 133317 | 0.022 | 133317 | 0.022 |
| 10 | 133288 | 133290 | 0.001 | 133290 | 0.001 |
| 20 | 133288 | 133288 | 0.000 | 133288 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=133288N,其中μ=1.0。
表 11‑12 :约束情况5:一端嵌固、一端自由(单位:N)
| 约束情况 | 一端嵌固、一端自由 | ||||
| 单元划分 | 理论解 | midas Gen | 相对误差(%) | MATLAB | 相对误差(%) |
| 1 | 33322 | 33573 | 0.753 | 33573 | 0.753 |
| 2 | 33322 | 33339 | 0.051 | 33339 | 0.051 |
| 5 | 33322 | 33323 | 0.003 | 33323 | 0.003 |
| 10 | 33322 | 33322 | 0.000 | 33322 | 0.000 |
| 20 | 33322 | 33322 | 0.000 | 33322 | 0.000 |
注:压杆临界承载力理论值:π2EI/(μl)2=33322N,其中μ=2.0。
【对比可知,MATLAB、SAP2000与midas Gen分析结果吻合很好,且随着单元细化,数值分析结果逐渐接近理论值。】
- 注释 ( Comments )
( 如果您发现有错误,欢迎批评指正。邮箱:jidong_cui@163.com . 如果您喜欢这篇博文,请在上面给我 点个赞 吧! 🙂 🙂
( If you found any mistakes in the post, please let me know. Email : jidong_cui@163.com. If you like this posts, please give me a “thumbs up“ rating on the above button! )
- 微信公众号 ( Wechat Subscription)
欢迎关注 “结构之旅” 微信公众号

