[FEM][MATLAB][有限元][编程] FEM Buckling Analysis Programming with MATLAB (Frame Elements) (框架单元曲屈分析编程)

Posted on by

坚持实干、坚持一线、坚持积累、坚持思考，坚持创新。

今天是20181231,2018年的最后一天，希望新的一年会更好。

接着博文《[力学][有限元][FEM]Basics of Buckling Analysis [曲屈分析基础]》继续介绍框架单元(Frame Element)用于屈曲分析的方法。该部分内容也是 书本 《有限单元法：编程与软件应用》屈曲分析章节的部分内容节选。

11.4 屈曲分析2：2D框架

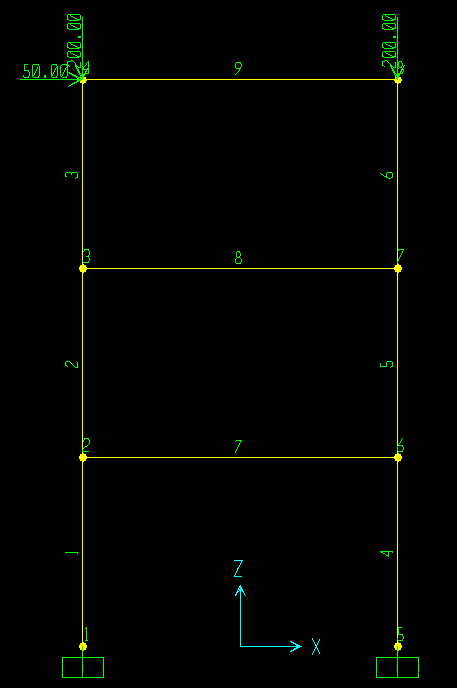
图 11‑7 结构模型示意

图 11‑7是本章的算例结构，是一榀平面框架结构，结构几何信息、构件属性和约束信息与第二章中静力分析时相同，荷载样式为：节点4处受到+x方向50kN的集中力和-z方向的100kN集中力作用，节点8受到-z方向的100kN集中力作用。本章将基于欧拉梁单元对该结构进行图中荷载样式下的屈曲分析，并将基于MATLAB编程计算的结果与SAP2000、midas Gen分析结果进行对比。

以下直接给出欧拉梁单元的几何刚度矩阵

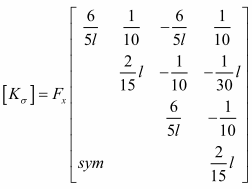             (11.4‑1)

其中Fx为单元轴力。

11.4.1 MATLAB代码与注释

屈曲分析的Matlab代码与前面章节中静力分析的Matlab代码略有不同，这里给出进行屈曲分析所需的主要代码。

% Frame 2D Buckling Analysis

% Author ： JiDong Cui（崔济东），Xuelong Shen（沈雪龙）

% Website : www.jdcui.com

% 20170609

……

此前代码与静力分析代码相同，不再赘述。

% Loading

force(10)=50;

force(11)=-200;

force(23)=-200;

……

根据图 11‑2，为相应的自由度施加荷载，作为参考荷载，用于后续求解单元的几何刚度矩阵。

% Solute balance function

disp('Displacement')

displacement(activeDof) = stiffness( activeDof , activeDof)\force(activeDof)

% Element force

disp('Force')

AxialForce=zeros(numEle,1);

for i=1:numEle

    noindex = EleNode(i,:);

    deltax = xx( noindex(2)) - xx( noindex(1));

    deltay = yy( noindex(2)) - yy( noindex(1));

    L = sqrt( deltax*deltax + deltay*deltay );

    C = deltax / L;

    S = deltay / L;

    T = [ C S 0 0 0 0;

         -S C 0 0 0 0;

          0 0 1 0 0 0;

          0 0 0 C S 0;

          0 0 0 -S C 0;

          0 0 0 0 0 1

    ];

    E = EList(EleSect(i));

    A = AList(EleSect(i));

    I = IList(EleSect(i));

    EAL = E*A/L;

    EIL1 = E*I/L;

    EIL2 = 6.0*E*I/(L*L);

    EIL3 = 12.0*E*I/(L*L*L);

    % Element stiffness matrix

    eleK = [ EAL   0    0    -EAL   0   0;

             0   EIL3  EIL2    0  -EIL3  EIL2;

             0   EIL2  4*EIL1  0  -EIL2  2*EIL1;

            -EAL   0    0     EAL  0     0;

             0   -EIL3 -EIL2    0   EIL3  -EIL2;

             0   EIL2  2*EIL1  0  -EIL2 4*EIL1

             ];

    eleDof = [noindex(1)*3-2 noindex(1)*3-1 noindex(1)*3 noindex(2)*3-2 noindex(2)*3-1 noindex(2)*3];

    ue=displacement(eleDof,:);

    uep=T*ue;

    fp=eleK*uep;

    AxialForce(i)=fp(4);

end

该段代码与普通静力分析的代码基本相同，主要用于计算参考荷载作用下单元的内力，用于后续计算单元的几何刚度矩阵，以下将介绍屈曲分析部分的主要代码。

% Geometric Stiffness Matrix

stiffnessM = zeros(numDOF);

stiffnessG = zeros(numDOF);

% Traverse all elements

for i=1:numEle;

    % Index of the element nodes

    noindex = EleNode(i,:);

    % Element length

    deltax = xx( noindex(2)) - xx( noindex(1));

    deltay = yy( noindex(2)) - yy( noindex(1));

    L = sqrt( deltax*deltax + deltay*deltay );

    % Element geometric stiffness matrix

    C = deltax / L;

    S = deltay / L;

    T = [ C S 0 0 0 0;

         -S C 0 0 0 0;

          0 0 -1 0 0 0;

          0 0 0 C S 0;

          0 0 0 -S C 0;

          0 0 0 0 0 -1

    ];

    % Section properties

    E = EList(EleSect(i));

    A = AList(EleSect(i));

    I = IList(EleSect(i));

    EAL = E*A/L;

    EIL1 = E*I/L;

    EIL2 = 6.0*E*I/(L*L);

    EIL3 = 12.0*E*I/(L*L*L);

    eleKm = [ EAL   0    0    -EAL   0   0;

             0   EIL3  EIL2    0  -EIL3  EIL2;

             0   EIL2  4*EIL1  0  -EIL2  2*EIL1;

            -EAL   0    0     EAL  0     0;

             0   -EIL3 -EIL2    0   EIL3  -EIL2;

             0   EIL2  2*EIL1  0  -EIL2 4*EIL1

             ];

    eleKgu=AxialForce(i)/L*[0,   0,       0,0,    0,       0;

                            0, 6/5,    L/10,0, -6/5,    L/10;

                            0,L/10,2*L^2/15,0,-L/10, -L^2/30;

                            0,   0,       0,0,    0,       0;

                            0,-6/5,   -L/10,0,  6/5,   -L/10;

                            0,L/10, -L^2/30,0,-L/10,2*L^2/15

                            ];

    eleKg=T'*eleKgu*T;

    % Corresponding freedom of the element nodes

    eleDof = [noindex(1)*3-2 noindex(1)*3-1 noindex(1)*3 noindex(2)*3-2 noindex(2)*3-1 noindex(2)*3];

    % Integrate element geometric stiffness matrix to the global geometric stiffness matrix

    stiffnessM( eleDof , eleDof) = stiffnessM( eleDof,eleDof) + T'*eleKm*T;

    stiffnessG( eleDof , eleDof) = stiffnessG( eleDof , eleDof) + eleKg;

end

本段代码主要作用：利用参考荷载作用下的单元内力，求解单元的几何刚度矩阵，进而采用“对号入座”的方式，将单元的几何刚度矩阵叠加，获得结构整体的几何刚度矩阵 [kσ] 。

% Solute

A=-stiffnessM(activeDof,activeDof)\stiffnessG(activeDof,activeDof);

[Vo,Do] = eig(A);        % Get the eigenvalues and eigenvectors

fo=diag(Do);

posneg=1./fo.*abs(fo);   

Vf=sortrows([Vo',abs(fo),posneg],size(Vo,1)+1);

V=Vf(:,1:size(Vo,1))';

f=Vf(:,size(Vo,1)+1).*Vf(:,size(Vo,1)+2);

fac=1./f

本段代码通过求解标准特征值问题，求得特征值和特征向量。Matlab内置函数 eig([A]) 可直接求解特征值和特征向量，求得的特征值放在向量 {Do} 中，相应的特征向量放在矩阵 [Vo] 中。其后的代码用于处理求解得到的数据，其中代码“V=”用于将特征向量排序，代码“f=”用于将结构自振频率进行排序，代码 “fac=” 用于求得屈曲因子，即特征值的倒数。图 11‑3所示是该桁架结构的前三阶屈曲模态。

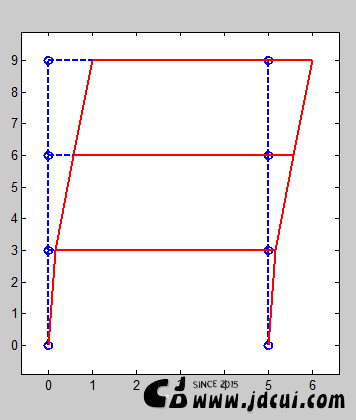
（a）第一阶

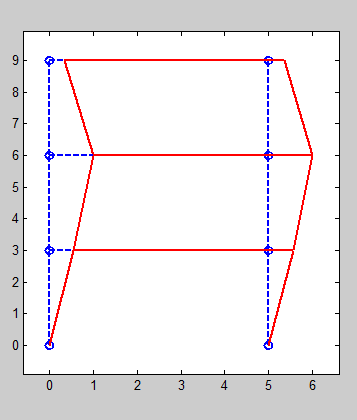
（b）第二阶

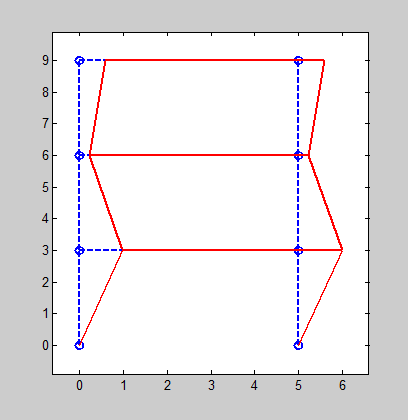
（c）第三阶

图 11‑8 框架结构屈曲模态

11.4.2 SAP2000分析结果对比

表 11‑2 给出了MATLAB分析的结构前6阶屈曲因子与SAP2000分析结果的对比，可以看出，两者吻合很好。

屈曲模态SAP2000结果MATLAB结果相对偏差（%）
174.69674.6960
2154.931154.9310
3302.256302.2560
4520.888520.8880
5786.546786.5460
6997.026997.0260
2D Frame Buckling SAP2000 vs. Matlab

表 11‑2 2D框架架屈曲分析结果对比

11.4.3 midas Gen分析结果对比

midas Gen模态分析过程与上节中桁架结构类似，此处不再赘述。midas Gen模态分析结果如图 11‑9所示，对比上述MATLAB分析结果与SAP2000分析结果，可见分析结果吻合很好。

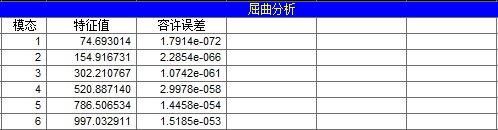
图 11‑9 midas Gen屈曲分析结果

You already voted!

  • 注释 ( Comments )

  ( 如果您发现有错误，欢迎批评指正。邮箱：jidong_cui@163.com . 如果您喜欢这篇博文，请在上面给我 点个赞 吧！ 🙂   🙂   

  ( If you found any mistakes in the post, please let me know. Email : jidong_cui@163.com. If you like this posts, please give me a “thumbs up“ rating on the above button! )

  • 微信公众号 ( Wechat Subscription)

WeChat_QRCode

欢迎关注 “结构之旅” 微信公众号

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.