[力学][有限元][FEM]Basics of Buckling Analysis [曲屈分析基础] (《有限单元法-编程与软件应用》章节节选)

实干、实践、积累、思考、创新。

11.1 稳定问题分类

结构失稳（屈曲）是指在外力作用下结构的平衡状态开始丧失，稍有扰动变形便迅速增大，最后使结构发生破坏。稳定问题一般分为两类，第一类是理想化的情况，即达到某种荷载时，除结构原来的平衡状态存在外，还可能出现第二个平衡状态，所以又称平衡分岔失稳或分支点失稳 (Buckling, Bifuraction)（图1中OAB曲线），对应于数学中是求解特征值问题，故又称特征值屈曲，此类结构失稳时相应的荷载称为屈曲荷载。第二类是结构失稳时，变形将迅速增大，而不会出现新的变形形式，又称极值点失稳(Instability)（图1中OCD曲线），结构失稳时相应的荷载称为极限荷载。此外还有一种跳跃失稳(Snap-through)（图1中OEF曲线），当荷载达到某值时（E点），结构平衡状态发生一个明显的跳跃，突然过渡到非临近的另一个具有较大位移的平衡状态（F点），由于在跳跃时结构通常已经破坏，其后的状态不能被利用，所以可归入第二类失稳。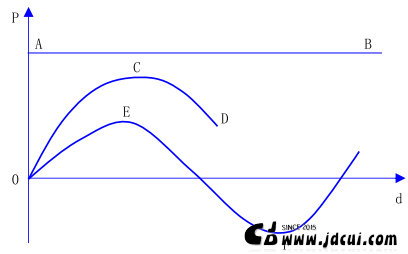

图 11‑1 稳定问题

11.2 最小势能原理

11.2.1 系统的平衡

若系统处于平衡状态，则一定存在一种位移状态，使得系统总势能为驻值，即

(11.2‑1)

公式中

(11.2‑2)

为系统总势能，U 为应变能，W 为外力功势能，数值上等于外力在系统变形中做的功取负值，三者都是系统位移的函数。

11.2.2 稳定平衡

如果要研究一个平衡是否稳定，则需要进一步考虑总势能的二阶变分条件，即

(11.2‑3)

工程中感兴趣的是临界平衡位置所确定的临界荷载和相应的屈曲形态，因此，总势能对位移的二阶导数为正的条件是研究弹性稳定性的理论基础。

11.2.3 弹性稳定问题的有限元列式

分析稳定问题时，需要在总势能的计算中考虑位移的高阶项影响，此时应变能U可以分为两部分，分别是应变能的线性部分和非线性部分，即

(11.2‑4)

外力功势能，则势能驻值方程可以写成

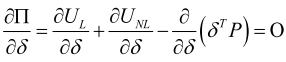(11.2‑5)

将应变能的线性部分和非线性部分分别写作

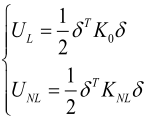(11.2‑6)

则势能驻值方程可进一步写成

(11.2‑7)

上式中，K₀ 一般是不变的，K_NL 与系统的位移及应力状态有关，因此该式是一个非线性方程。如果以未变形的初始位移为参考，则K_NL 只与系统的应力有关，此时这种仅由应力状态所决定的单元刚度矩阵叫做几何刚度矩阵，或初应力矩阵，用Kσ表示。

11.2.4 弹性稳定问题的求解

弹性稳定问题可分为两类，一类是欧拉稳定问题，另一类是极值稳定问题。

欧拉稳定问题是指系统的初应力状态处于某种临界状态时，对于临界位移的任何挠动都可能使系统丧失稳定性。如果把欧拉失稳的临界状态看成是一种初应力状态，则欧拉稳定问题也可用公式 (11.2‑7) 求解。具体为：根据某一初始应力状态{σ} ，求得几何刚度矩阵[Kσ]，同理易知当初始应力状态为λ{σ} 时，几何刚度矩阵为 λ[Kσ]，则公式(11.2‑7) 可写作

(11.2‑8)