Finite Element Method [有限元法] / Structural Analysis [结构分析] / Structural Design [结构设计] / Structural Engineering [结构工程]

[结构力学][笔记] 不同支座条件的斜梁的受力分析(两道结构力学题)(楼梯板)

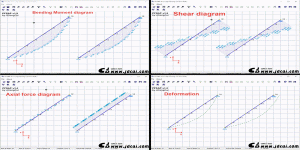
坚持实干、坚持实践、坚持积累、坚持思考，坚持创新。 和小伙伴讨论斜梁的挠度计算问题，然后想到了两个斜梁的计算。直接用上图说话吧。 采用PFSAP （ [有限元][编程][日记] PFSAP：平面框架弹性静力分析程序 ）进行计算，如下： 两个斜梁，主要区别是支座条件不同。左边梁是两端铰接，右边梁底部支座是铰接，顶部支座只约束竖向平动。 弯矩图 剪力图 轴力图 支座反力 变形图 由以上分析可见，左边梁和右边梁 弯矩图和剪力图是一样的，但左边梁没轴力，右边梁有轴力。同时变形图也不一样。左边梁其实是一个斜着放的简支梁。 另外，如果把这两根梁平着放，那受力状态就完全一样了，即便右端支座约束不同。因为平着放的时候，在竖向力作用下，水平向无伸长，支座水平向是否有约束不影响结果。 欢迎关注 “结构之旅” 微信公众号

Finite Element Method [有限元法] / Mechanics [力学] / Midas / Steel Structure [钢结构] / Structural Analysis [结构分析] / Structural Engineering [结构工程]

[FEM][Midas Gen] 四边简支板的受压屈曲分析(Compress Buckling Analysis of a Simply Supported Plate)(有限元及弹性力学解)

坚持实干、坚持一线、坚持积累、坚持思考，坚持创新。 分析用Mdias Gen，正方形四边简支板，受侧向单位线荷载作用，进行屈曲分析。 第1阶 临界荷载系数：7.449E+002 X方向及Y方向均屈曲为1个半波，也即最容易失稳的模态。 第2阶 临界荷载系数：1.164E+003 X方向屈曲为2个半波及Y方向均屈曲为1个半波 第3阶 临界荷载系数：2.072E+003 X方向屈曲为3个半波及Y方向均屈曲为1个半波 第4阶 临界荷载系数：2.982E+003 X方向屈曲为2个半波及Y方向均屈曲为2个半波 第7阶 临界荷载系数：4.662E+003 X方向屈曲为1个半波及Y方向均屈曲为2个半波。 PS.第7阶才才轮到X方向屈曲为半个波形。 第10阶 一阶屈曲临界荷载弹性力学解为744.739与有限元分析结果7.449E+002一致。 验算如下： Ncr = Kπ2Et(t/b)2/12(1-v2) = 4 * 3.14159262*2.06*105*10*(10/1000)2/12/(1-0.32)=744.739 微信公众号 ( Wechat Subscription) …