[软件][振动控制] FOUR_TRAN 案例7: 钢楼梯实测振动数据(不同频率成分对加速度峰值的贡献) (FOUR_TRAN Ex7: Frequency spectrum of measured vibration data of Steel stairs)
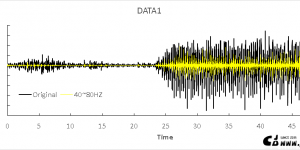
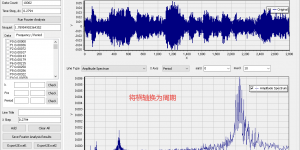
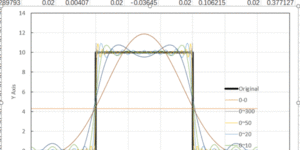
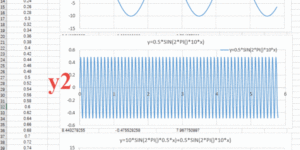
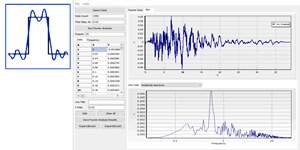
实干、实践、积累、思考、创新。 最近参与的一个钢楼梯振动舒适度控制的项目,实测了钢楼梯在不同加载工况下的加速度时程。 在处理数据的时候发现,有些实测曲线整体看来变化较为平稳,有些曲线则会在局部出现一些零散的突兀点,而最大值往往就是这些突兀点控制。 下面是两组这样的曲线,第一组是相对平稳的曲线,第二组是存在明显零散的突兀点。 Data1 Data2 第一直觉,这些突兀点应该是高频成分导致。我们可以采用( [数学][地震动][软件] FOUR_TRAN: Fourier Analysis Tool [傅里叶分析工具] )对其他进行频谱分析,并通过滤波处理,获得不同频率成分的加速度时程,进行对比。 把数据导入FOUR_TRAN,进行分析如下。 第一组曲线不同频率成分的加速度时程曲线 第二组曲线不同频率成分的加速度时程曲线 汇总不同频率成分加速度曲线峰值 由以上分析可见: (1)第二组数据的高频成分比第一组数据大,40HZ~80HZ成分占据了加速度峰值达到原始数据的79.3%,远大于第一组数据的43.1%。 (2)对于第二组数据,零散的突兀点是高频成分所致!高频成分对加速度峰值贡献极大!! (3) 如果以峰值作为一个评价指标,这个时候高频成分的来源分析就特别重要。如果高频成分是真实的,比如一些附属结构引起,那就必须以实测值为准。如果高频成分是仪器不稳定引起,或者是测试时候受一些异常操作影响,那就应该过滤掉再进行评估。 (4)最后的最后,舒适度需要以真实体感结合为主,数字只是数字。 相关博文 ( Related Topics) [00] [数学][地震动][软件] …