实干、实践、积累、思考、创新！ Tag: 结构工程博士 结构工程师 程序员 结构抗震设计 振动控制 光伏支架 加固改造 软件研发 编程 弹塑性 有限元 超高层 超限设计
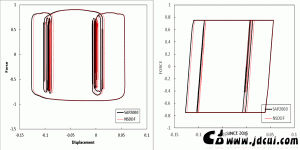
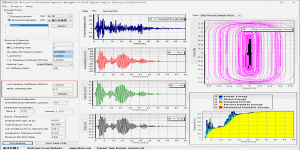
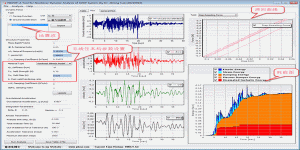
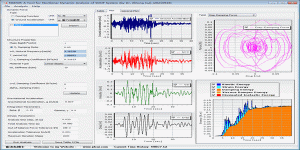
实干、实践、积累、思考、创新。 程序图标 ( Program Icon ) 程序介绍 ( Program Introduction) 地震反应谱是地震工程中重要的概念，我们经常需要将地震加速度时程转换为反应谱。SPECTR 是一个简单易用的反应谱计算程序。 Seismic Response Spectra is an important concept in earthquake engineering, we often need to evaluate seismic response spectrum on the basis of …
新版已推出，请移步：[软件][编程][动力学] NSDOF v2023: A Tool for Nonlinear Dynamic Analysis of SDOF System (NSDOF单自由度系统动力非线性分析工具 v2023) 实干、实践、积累、思考、创新。 趁着国庆，来个大更新，再2020版NSDOF的基础上，增加了非线性黏滞阻尼器、摩擦阻尼器、黏弹性阻尼器、金属阻尼器，适合做减震研究。 程序图标 ( Program Icon ) 程序介绍 ( Program Introduction) NSDOF 是一个基于微软的windows窗口程序，用于单自由度结构的动力非线性分析。结构可是弹性也可以是弹塑性。动力荷载可以是施加在结构基座的地震加速度，也可以是施加在结构顶部的动力荷载。程序使用逐步积分法求解增量非线性运动方程。可以输出结构的各种响应结果，包括抗力，阻尼力，参考惯性力，位移，速度，加速度，耗能，滞回曲线等。 NSDOF is a …
实干、实践、积累、思考、创新。 马上更新……(ps. 2018年12月写下的题目， 相关博文( Related Topics) [01]. [Tool] SPECTR – A program for Response Spectra Analysis [反应谱计算程序] [02]. [程序][Tool] Ground Motion Selection [强震记录选取] [03]. [程序][软件]Ground Motion Library [强震记录管理] [04]. Artificial ground …
实干、实践、积累、思考、创新！ 粘弹性阻尼器是一种有效的减震控制装置，主要依靠粘弹性材料的滞回耗能，为结构提供附加刚度和阻尼，减小结构动力反应，从而实现减震目标。粘弹性阻尼器既能提供刚度，也能提供阻尼，其典型的滞 回曲线为椭圆形，具有良好的耗能性能。下图 所示是粘弹性阻尼器的滞回环形状示意。 粘弹性阻尼器，恢复力由两部分构成，即速度相关部分和位移相关部分，具体如下 NSDOF提供了单自由度主体结构及黏弹性阻尼器并联的动力时程分析模型，以下做两个测算。 第一个算例，结果部附加任何阻尼器，结构刚度取10，阻尼比取0.05，对应的阻尼系数为0.15915，点击运行计算可获得对应的力、位移响应结果及能量图。由能量图可见，此时主要包含3种能量：动能+应变能+阻尼耗能 第二个算例，主体结构的阻尼取0，刚度取一个很小的值0.0001，几乎可忽略，同时设置黏弹性阻尼器的阻尼系数为0.15915，与算例1中的主体结构的阻尼系数一致，黏弹性阻尼器的刚度取10，鱼算例1中的主体结构的刚度一致。因此可知，算例2的计算结果应该与算例1是一致的，相当于用一个黏弹性阻尼器去等效一个单自由度系统。计算结果如下图所示。 由结果可见，算例2的位移、速度、加速度响应均是与算例1一致的。不同的是，算例2的能量图，此时主要包含2种能量：动能+黏弹性阻尼器的耗能，因为用黏弹性阻尼器等效算例1的主体结构，同时也可以发现，黏弹性阻尼器的耗能等于算例1主体结构的应变能及阻尼耗能的叠加。 另外从滞回曲线可以发现，黏弹性阻尼器的滞回曲线是椭圆。此时黏弹性阻尼器的滞回曲线也等于算例1主体结构他弹性恢复力滞回曲线及阻尼力滞回曲线的叠加。 相关话题 ( Related Topics) [01]. [Tool] SPECTR – A program for Response Spectra Analysis [反应谱计算程序] [02]. [程序][Tool] Ground Motion Selection [强震记录选取] [03]. [程序][软件]Ground Motion …
实干、实践、积累、思考、创新。 介绍 NSDOF ( [软件][更新][Dynamics] NSDOF v2021: A Tool for Nonlinear Dynamic Analysis of SDOF System (NSDOF单自由度系统动力非线性分析工具 v2021) ) 设置摩擦阻尼器的单自由度体系动力时程分析。简单来个step by step图片演示吧。 STEP 1： 导入一个震荡动力荷载 STEP 2： 假定主体结构为弹性，设置摩擦阻尼器的摩擦力及刚度。 STEP 3： 点击Run …
实干、实践、积累、思考、创新。 在网友建议下，NSDOF ( [Tool][软件][Dynamics] NSDOF v2020: A Tool for Nonlinear Dynamic Analysis of SDOF System (NSDOF单自由度系统动力非线性分析工具 v2020) ) 增加了非线性粘滞阻尼器。可以在考虑或者不考虑结构阻尼的情况下，考虑非线性粘滞阻尼器进行动力时程分析。下面算例测试NSDOF同时设置非线性粘滞阻尼器+材料非线性的动力时程分析功能，同时用SAP2000进行同样的分析，并对比验证。其中非线性阻尼器阻尼指数取0.1，整个动力方程高度非线性。 算例参数 质点质量： 1kg 体系弹性刚度：100N/m 屈服强度： 0.75N 屈服后刚度强化系数：0 结构的粘滞阻尼系数c：0N-s/m 粘滞阻尼器的阻尼系数cvd: 1.0 N-s/m …
实干、实践、积累、思考，创新。 在网友建议下，NSDOF ( [Tool][软件][Dynamics] NSDOF v2020: A Tool for Nonlinear Dynamic Analysis of SDOF System (NSDOF单自由度系统动力非线性分析工具 v2020) ) 增加了非线性粘滞阻尼器。可以在考虑或者不考虑结构阻尼的情况下，考虑非线性粘滞阻尼器进行动力时程分析。下面做两个算例测试一下NSDOF的非线性粘滞阻尼器计算功能，同时用SAP2000进行同样的分析，并对比验证。 算例1：线性粘滞阻尼 具体参数： 质点质量： 1kg 体系弹性刚度：100N/m 结构的粘滞阻尼取 ：0 粘滞阻尼器的阻尼系数c: 1.0 N-s/m 粘滞阻尼器的阻尼指数alpha：1.0 …
实干、实践、积累、思考、创新。 最近小伙伴做非线性粘滞阻尼器的参数分析，于是我们在 NSDOF （http://www.jdcui.com/?p=13947）软件上加了非线性粘滞阻尼器的分析功能。顺便做些测算例子。 这个例子与前面[软件][动力学][Dynamics] NSDOF算例1——单自由度体系弹性动力时程分析 例子的模型基本一致，不同之处在于此例结构为非线性，取二折线非线性本构，进行非线性动力时程分析。 单自由度体系参数： 质量m: 1.0 N-s2/m (kg); 阻尼比: 0.05； 初始刚度k0: 10 N/m; 屈服强度Fy: 0.75N 相应的屈服位移为 0.075m 重力加速度g: 9.807 m/s2; 加速度时程： A9OL 对应的阻尼系数c: 0.31623 N-s/m, 单自由度体系的自振周期为 …
实干、实践、积累、思考、创新。 最近小伙伴做非线性粘滞阻尼器的参数分析，于是我们在 NSDOF软件 （http://www.jdcui.com/?p=13947）上加了非线性粘滞阻尼器的分析功能。顺便用NSDOF做些测算例子。这是一个单自由度体系动力分析的例子。 单自由度体系参数： 质量m: 1.0 N-s2/m (kg); 阻尼比: 0.05； 弹性刚度k: 10 N/m; 重力加速度g: 9.807 m/s2; 加速度时程： A9OL 对应的阻尼系数c: 0.31623 N-s/m, 单自由度体系的指针周期为 1.98692s 采用NSDOF进行计算，设置参数，并分析 同时采用NONLIN进行计算，并对比验证。 时程结果对比 NONLIN的结果 NSDOF的结果 滞回曲线结果对比 …
实干、实践、积累、思考、创新。 《建筑抗震设计规范》（GB50011-2010）中给出了采用振型分解反应谱法计算地震作用时的地震力计算公式：\({F_{ji}} = {\alpha _j}{\gamma _j}{X_{ji}}{G_i}\)，其中\({\gamma _j} = \frac{{\sum\limits_{i = 1}^n {{X_{ji}}{G_i}} }}{{\sum\limits_{i = 1}^n {X_{ji}^2{G_i}} }}\)，\({F_{ji}}\)为j振型i质点的水平地震作用标准值；\({\alpha _j}\)为相应于j振型自振周期的地震影响系数；\({X_{ji}}\)为j振型i质点的水平相对位移；\({\gamma _j}\)为振型的参与系数。以下根据结构动力学的相关理论，给出上述公式的一种推导。 1多自由度体系振型分解法 Mode Superposition Method 对于多质点体系，地震动力方程为： $${\left[ M \right]\left\{ {\ddot u} \right\} …
实干、实践、积累、思考、创新。 最近研究舒适度，做些算例测算。对两端铰接、两端固接、一端固接一端铰接、悬臂等截面梁进行振型分析，获得各类梁的前三阶振型，并对振型向量进行最大位移值归一化，并利用归一化后的振型向量求解前3阶振型的振型质量。测试算例梁截面统一为，梁截面为200X200，梁长度为1000mm，沿梁长划分80个单元，振型的质量通过公式 \({M_n} = \int_0^L {m(x)\phi _n^2(x)dx} \) 进行计算。 1 简支梁 1.1 振型形状 一阶振型 二阶振型 三阶振型 1.2 振型质量 振型 节点质量 总质量 振型质量 振型质量/总质量 1 0.0009815 0.314 0.1570 0.500 2 0.0009815 …
坚持实干、坚持积累、坚持思考，坚持创新。 题目如题，结论肯定是没有影响的，因为振型向量本来就是不定的，振型元素之间只有相对关系，要求解振型向量元素的具体值，必须对振型向量进行标准化。简单说即先假定某个元素的值，然后才能求解出其余元素的值。 最近在研究舒适度，顺便把相关东西整理一下，正好还有小伙伴问，同时正好测试一下在网站上用LATEX写公式，看看是不是会专业点。 基本公式 结构的运动方程： \[[M]\{ \ddot u\} + [C]\{ \dot u\} + [K]\{ u\} = \{ P\} （公式1） \] 将位移向量\(\{ u\} \) 用振型展开， \[\{ u\} = [\phi ]\{ q\} …
实干、实践、积累、思考、创新。 最近研究舒适度，涉及振型向量的标准化，顺便测试一下SAP2000默认的振型向量标准化方法。 大家都知道，振型向量是不定的，振型向量的参数之间只有比值关系。为了求解振型向量的元素绝对值，必须对振型向量进行标准化。 我们接下来测试SAP2000中振型向量的标准化方法，在SAP2000中建立一根简支梁模型，如下图： 梁的前三阶Z向振型形状如下： 振型形状是与理论分析结果一样的。 将软件输出的振型变形的平方乘以节点质量，可获得各振型的广义质量，结果均为1。即SAP2000默认输出的振型是满足关于质量矩阵内积为1的条件的。即采用的是关于质量矩阵的正交归一化方法。 相关博文( Related Posts ) [01] [Structural Dynamics][Mode superposition] 振型参与质量系数(Participating Mass Ratio) [02] [动力学][振型分解][Mode Superposition] 振型向量与振型参与系数的乘积公式推导 [03] [结构设计][地震作用][规范] 振型分解反应谱法的一些概念总结 (Basic Concepts of Response Spectra …
实干、实践、积累、思考、创新。 如题，一看是一个莫名其妙的想法。实际上也是一个错误的想法，不过，当时脑子一热，就测算一下。具体看看结果。 模型： 20层的剪切层模型。 阻尼矩阵： （1）模态阻尼，20阶振型计算 （2）模态阻尼，20阶振型计算，把非对角线元素取为0。 采用MATLAB编程，采用Newmark-β积分法进行弹性时程分析，两种阻尼模型的计算结果对比如下。 其中，参考阻尼为完整的模态阻尼，对比阻尼为去掉阻尼矩阵对角线元素后的矩阵。 由图可见，采用仅保留对角线元素的阻尼矩阵，结构的位移及剪力响应远小于完整的阻尼矩阵，而楼层加速度响应似乎相差不大！！十分诧异！！ 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号
实干、实践、积累、思考、创新。 对于整体结构，X向地震作用下，结构有Y向的剪力吗？以下通过两个简单的时程分析案例进行测算。 案例1： 振型结果如下： 振型1为Y向平动 振型2为X向平动 振型3为绕Z轴扭转 案例2：案例1模型逆时针旋转45度 周期值与模型1是一样的，只是因为结构转了一个角度，振型方向不同了。 振型1为135度方向平动 振型2为45度方向平动 振型3为绕Z轴的扭转 分别对两个模型沿X向施加地震动加速度时程，进行直接积分动力时程分析。所选的地震波如下图所示。 模型1沿X方向与Y方向的基底剪力结果如下图所示。由图可知，对于模型1，沿X向输入地震，Y向剪力几乎为0。 模型2沿X方向与Y方向的基底剪力结果如下图所示。由图可知，对于模型2，沿X方向输入地震，结果Y向会产生剪力，且剪力大小不可忽略。 粗看似乎有点难理解，外力和内力不是应该平衡的吗？为何施加X方向加速度，结构有Y向的剪力？对于静力情况下，结构受到到的外力与的内力平衡，比如，当沿结构X方向施加力F时，结构总的剪力必然是沿X方向，且大小为F，Y方向不存在剪力。为何到了动力情况，就不满足这个规律了？不妨看一下两种情况下结构的平衡方程。 结构静力平衡方程： 其中，为结构的外力，为结构的抗力，其中，当只有X向力作用时，即 ，，即结构的抗力也只有X反向的力，y及z向的力为0 结构动力平衡方程（地震）： 其中，当只有x向地震时，，即向量在非X向自由度上为0，此时结构的抗力，假设忽略阻尼，结构的抗力为，对比静力平衡下的公式（）可见，尽管向量在非X向自由度上为0，但是抗力的右边项不是，而是，即所谓的绝对加速度，其中相对加速度在非X向自由度上不一定为0，当在非X向自由度上存在非0值时，抗力就可以能存在非X向自由度上的力，即对于整体结构，X向地震作用下，结构整体在其他方向也可能存在抗力，包括Y向的剪力。 对于算例1，在X向地震加速度作用下，由于结构基本只有X向的位移，因此Y向的抗力很小，进而Y向剪力很小。对于案例2，由于结构扭转了45度，在X向地震加速度作用下，结构不仅有X向的位移，也有Y向的位移，有Y向的位移，就可能有Y向的抗力及Y向剪力。 由以上分析也可发现，引起动力与静力概念上不同的错觉的原因是，把动力情况下结构的抗力当成了，实际上动力情况下结构的抗力等于（忽略阻尼情况下）。 平衡还是满足的！！！。 相关博文 ( Related Topics) [01] …
坚持实干、坚持实践、坚持积累、坚持思考，坚持创新。 复习基本知识，整理资料。振型分解法。 （1）振型向量是有量纲的。量纲为长度的倒数。 （2）振型向量关于质量矩阵正交。 （3）振型向量与振型参与系数的乘积为荷载指向向量。推到过程中利用到分块矩阵的一些计算。 相关博文(Related Topics) [01] [Structural Dynamics][Mode superposition] 振型参与质量系数(Participating Mass Ratio) [02] [动力学][振型分解][Mode Superposition] 振型向量与振型参与系数的乘积公式推导 [03] [结构设计][地震作用][规范] 振型分解反应谱法的一些概念总结 (Basic Concepts of Response Spectra Method) [04] [动力学][SAP2000] SAP2000中振型向量的标准化方法 …
本书前面章节主要介绍了PEROFRM-3D中常用非线性组件和单元的基本属性与应用，旨在建立正确的结构弹塑性分析模型。本章则侧重于介绍结构整体弹塑性分析模型的建立、结构整体动力弹塑性时程分析的步骤及运用PERFORM-3D[1,2]进行结构抗震性能评估的流程。
ANSYS 影响线分析。(Influence line analysis using ANSYS)
ANSYS 框架结构模态分析练习。(This is a small example to outline the steps required to do a simple modal analysis of a frame structure using ANSYS.)
Abaqus框架结构模态分析练习。(This is a small example to outline the steps required to do a simple modal analysis of a frame structure using Abaqus.)
SDOF是一个基于微软的windows窗口程序，用于单自由度结构的动力非线性分析。结构可是弹性也可以是弹塑性。动力荷载可以是施加在结构基座的地震加速度，也可以是施加在结构顶部的动力荷载。程序使用逐步积分法求解增量非线性运动方程。SDOF is a Microsoft Windows based application for the dynamic analysis of single degree of freedom structural systems. The structure may be modeled as elastic, elastic-plastic. The dynamic loading may be input as an earthquake accelerogram acting at the base of the structure, or as a dynamic force applied at the roof of the structure. The program uses a step-by-step method to solve the incrementally nonlinear equations of motion.
[01] Ground Motion Selection (选波) 服务
[02] 著:《PERFORM-3D原理与实例》
[03] 著:《有限单元法-编程与软件应用》
[04] 著:《结构地震反应分析-编程与软件应用》
[05] 著:《有限单元法 Python编程》（New!!!）
[06] Software Notes [软件笔记汇总]
[07] 土木工程试验数据处理软件汇总（New!!!）
[08] 自编程序 [Software Box]（New!!!）
[09] 手绘大样 [Detail Drawing]（New!!!）
