[动力学][结构] 大震弹塑性顶点位移时程为何”不收敛”?[Why does the displacement time history of earthquake elastic-plastic analysis not converge?]
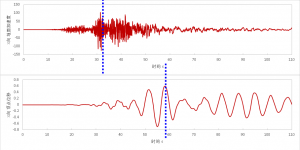
实干、实践、积累、思考、创新。 经常碰到小伙伴做完大震弹塑性分析后,跑过来问为何结构顶点位移总是不收敛? 怎么个不收敛法?大家看看下面这个图: 上述两组图中,上方的是结构某主方向的地面加速度(总时间110s),下方的是结构对应方向的顶点位移时程曲线(算到60s)。 由图可见:其中地面峰值加速出现在30~40s,在60s时地面加速度已退化为峰值的30%以上,而结构顶点位移算到60s依然不减衰减。地面加速度衰减速度很快,加速度峰值明显靠前,而顶点位移似乎还没出现峰值,看起来“发散”。为何加速度已经显著退化,而位移还没收敛? 最初看到这类曲线的时候,也很诧异?后面思考后发现,之所以会存在这种诧异,是因为我们对比的基准选错了。 上面的例子中,我们拿结构的顶点位移时程和地面加速度进行对比?实际上,加速度和位移之间差了两次积分,加速度峰值和位移峰值并不一定出现在同时刻,两者本身可以差很大。 对比结构顶点位移时程的趋势参照地面的位移时程更直观,而不是参照地面加速度时程。位移与位移对比才直接。 以上图中的加速度为例,我们对加速度进行积分,获得对应速度与位移时程,结果如下图所示。 由上图可见,X向和Y向的地面加速度时程峰值分别出现在30s和40s左右,而对应的位移时程峰值分别出现在50s和55s,足足推后了15~20s左右。 从这个角度来看,顶点位移要出现明显退化,加速度应该算到60s,甚至可能更多。为此我们把弹塑性分析时间直接设置为110s的时间,再次提取顶点位移时程结果,如下图所示。 有上图可见,在60s后,两个方向的顶点位移均开始出现不同程度的退化。由于我们通常进行的是一致地震激励计算,因此超限报告中,往往只给出加速度时程曲线,并没有提供地面位移时程曲线,让人很自然地采用地面加速度时程对比顶点位移时程进行参照,从而引起了上述诧异。 有了这样的发现,我们不妨找几组天然地震记录进行积分计算,看看这些地震加速度时程曲线的“显著退化点”和地面位移时程曲线的“显著退化点”出现的位置情况。 这里曲线的“显著退化点”定义为曲线正向最大值和负向最大值中靠后出现的那个。 由上述多组图可见: (1)地面加速度时程曲线的抖动程度最大,经过二次积分后得到的位移时程曲线变得平缓,速度时程曲线的抖动程度次之。 (2)地面加速度、速度、位移曲线的“显著退化点”出现位置不同,三个曲线的“显著退化点”出现的位置先后关系不定,但从选取的几组天然地震波的分析结果来看,速度时程曲线和加速度时程曲线的“显著退化点”相对较为接近,而地面位移时程曲线的“显著退化点”与加速度时程曲线的“显著退化点”可能相差较远,且位移曲线的“显著退化点”更靠后。 (3)对比结构顶点位移时程的趋势参照地面的位移时程更直观,而不是参照地面加速度时程。 相关博文( Related Topics) [01]. [Tool] SPECTR – A program for Response Spectra Analysis …