[振动控制][软件] VCAP: Vibration Comfort Assessment Program [振动舒适度评估软件]
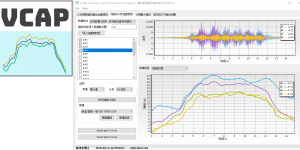
实干、实践、积累、思考、创新。 程序图标 ( Program Icon ) 程序介绍 ( Introduction) 轨道交通环境振动影响评价标准是确定振动评价方法、指标和限值的关键,总结近年来轨道交通环境振动相关标准和规范,对轨道交通环境振动范畴、振动描述与测量基本参量和振动预测与控制方法进行梳理,编制了VCAP: Vibration Comfort Assessment Program 振动舒适度评估软件 程序,用于对常用的振动指标进行计算分析与评估,是进行振动分析研究及相关振动项目设计的好帮手。 VCAP 可满足常用规范及标准的要求,这些规范主要涉及: 1)《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》: JGJT 170―2009 . Standard for limit and measuring method of building vibration and …
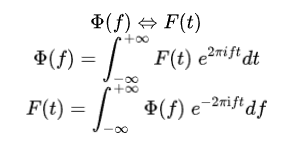
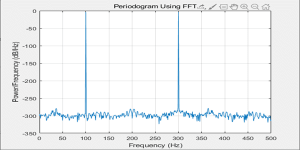
 ) 后仔思考发现,主要是因为功率谱使用了 分贝 为计量单位,比如通过公式 10*log10(Pxx) 将原本的功率谱Pxx进行转换,可见当Pxx处于0~1之间的时候,通过log10(Pxx)转换出来的公式就是负数了。 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号
) 后仔思考发现,主要是因为功率谱使用了 分贝 为计量单位,比如通过公式 10*log10(Pxx) 将原本的功率谱Pxx进行转换,可见当Pxx处于0~1之间的时候,通过log10(Pxx)转换出来的公式就是负数了。 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号