[数学][笔记] 随机过程中的平稳与各态历经 (Stationarity and ergodicity in random processes)
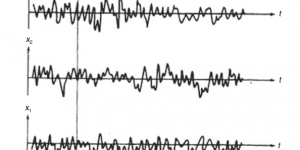
实干、实践、积累、思考、创新。 学习随机振动分析需要搞清楚 两个最重要的随机过程特性:平稳性(Stationarity )及各态历经(ergodicity )。 [平稳性] 指的是随机过程的概率特性(如期望值、自相关函数等)与时间无关。 [各态历经] 各态历经也称为遍历性,指的是一个平稳随机过程任意样本函数的时间平均都相等,且等于集合的平均。其最大作用是,有了各态历经假定,意味着可以通过对一个具体的样本进行分析,获得总体集合的概率特性。 一个随机过程具有平稳性,则描述起来大大简化,比如,只需要用一个概率密度函数描述各个时间点的概率分布特性,因为随机过程的概率特性不随时间改变。很多非平稳随机过程的研究,也采用以平稳过程为研究入手,然后通过某种方式进行非平稳随机修正。 如果一个平稳随机过程具有各态历经性,同样可以大大简化随机过程的分析。如前所述,有了各态历经假定,意味着可以通过分析一个具体的样本的方式获得总体集合的概率特性。如果没有各态历经,要获得随机过程的概率特性,则需要足够大的样本,进行样本间统计,这在大多数实际情况均不具备可行性。 终上所述,平稳及各态历经特性是比较理想的,并不是所有随机过程都满足,但从某种程度上讲,随机过程具有平稳及各态历经特性,研究才具有可行性啊。 相关博文( Related Topics) [01] [笔记] 随机过程中的平稳与各态历经 (Stationarity and ergodicity in random processes) [02] [振动控制] 常见质量阻尼器分类 [Passive, semi-active, active and …