[PERFORM-3D] PERFORM-3D中阻尼怎么取值?
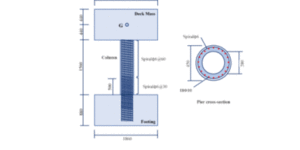
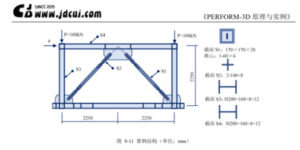
实干、实践、积累、思考、创新 读者在看《PERFORM-3D原理与实例》(http://www.jdcui.com/?page_id=3757)一书时问我这个问题,今天抽时间整理了一下,如果我回答有问题,欢迎大家批评指正。 读者问题:“PERFORM-3D中阻尼参数怎么取?常用的结构体系如钢筋混凝土结构、钢结构、型钢混凝土结构的阻尼比怎么取值?“ 答: (1)p3d中,建议用模态阻尼+瑞丽阻尼的组合方式进行动力分析,你刚才界面显示的是瑞丽阻尼。为何这样处理?因为我们小震分析用的是反应谱法,各振形指定阻尼,这个阻尼组装成矩阵对应的阻尼就是模态阻尼。而p3d中,也提供了这个选项,但完整的模态阻尼阶次是与动力自由度数量一致的,除非把所有模态求出来,才能组合成完整的模态阻尼,而实际弹塑性动力分析的时候不可能求太多阶模态,因为计算效率问题,所以就取前面主要的模态数量,而放弃后面的模态,比如p3d模态分析的最多好像只允许60阶,那舍弃掉的就是部分高频阻尼,因此,开发者建议,这里仅是象征性增加一点瑞丽阻尼,如上图的0.1%,同时有利于收敛性,有利于收敛性。具体取值对总体结果影响不大。 (2)三种结构阻尼比怎么取,按整个结构取一个统一阻尼比其实是最早的提法,整体结构笼统一般仅适用于纯质材料,如常规混凝土结构取0.05,纯钢结构0.03,可能都没太多异议。但到了混合结构怎么取,就头疼了,因为分不清材料多少。其实目前大部分弹性分析软件,包括YJK,midas Gen 都提供了基于材料应变能的阻尼比计算方法,你直接指定材料的阻尼比,软件会基于材料应变能算出各阶振型的阻尼比。对于混合结构,你会得到各阶振型下的阻尼比,然后各阶振型按不同的阻尼比直接进行反应谱计算。 (3)因此回到实际情况,倘若你p3d做的是混合结构,建议你在yjk中用材料应变能进行分析,得到前面主要各阶模态的阻尼比,然后再取一个合理值,在p3d中通过模态阻尼比进行指定。因为貌似p3d不能按振形分别指定阻尼比,只能所有模态统一指定一个阻尼比。 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号