[软件][地震动][更新] GMP v2024: A tool for Calculating Ground Motion Parameters for Seismic Analysis of Structures [结构抗震分析地震动强度指标/地震动参数计算工具]
实干、实践、积累、思考、创新。 程序图标 ( Program Icon ) 程序介绍 ( Program Introduction) GMP ( A tool for Calculating Ground Motion Parameters for Seismic Analysis of Structures) 是一款结构抗震分析地震动强度指标/地震动参数计算工具,程序将地震波积分+反应谱分析+地震动参数分析等功能集合于一身,使用方便。GMP的主要功能包括: (1) 丰富的地震波数据格式导入支持 (2) 地震动加速度、速度、位移时程 (3) 地震加速度谱计算功能,包括伪加速度谱、速度谱、位移谱 (4) …
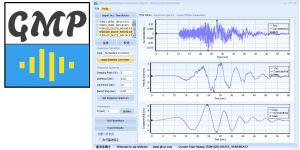
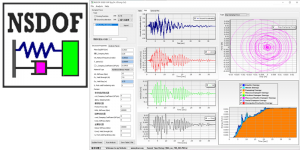
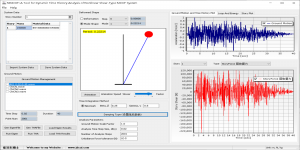
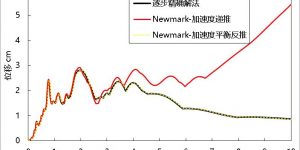
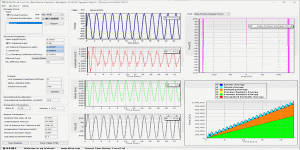
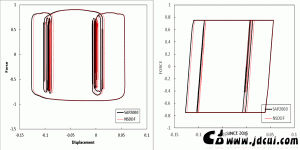
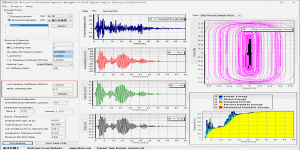
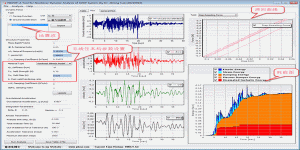
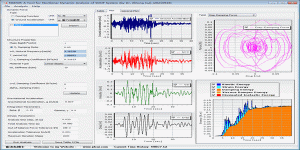
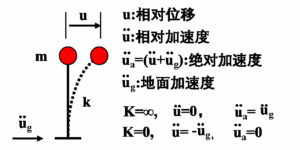

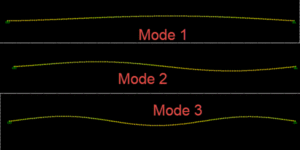
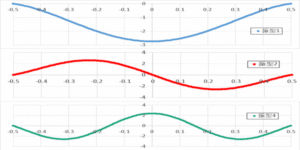
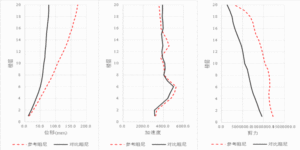
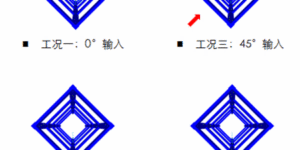
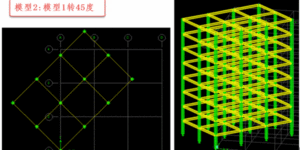
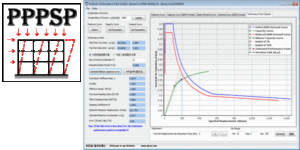
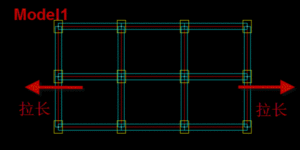
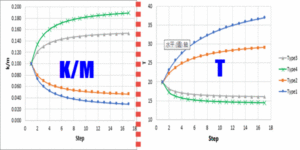
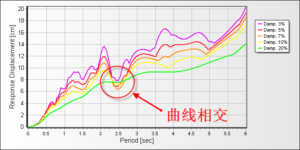

 图 1 图 2 图3 图 4 图 5 图 6 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号
图 1 图 2 图3 图 4 图 5 图 6 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号