[数学][笔记] 傅里叶变换公式的几种形式 (Several Forms of Fourier Transform Formulas)
实干、实践、积累、思考、创新。 # 傅里叶变换公式的几种形式 研究振动控制、随机振动等,离不开傅里叶变换(Fourier transforms)。对于傅里叶变换,不同文献、书籍有时候会采用不同形式的公式,刚开始看的时候有点凌乱,后面才理清楚,其实不同公式形式本质上都是等价。为了便于后续学习,以下总结几种常见的傅里叶变换公式形式。PS.这里傅里叶变换,指的是非周期函数(周期可以理解为无限长)的傅里叶变换,不是傅里叶级数(Fourier series),傅里叶级数是针对周期函数的说法。 ## 第一种形式 一种通用的形式,\(\Phi \left( p \right)\)和\(F\left( x \right)\)互为傅里叶变换对: $$\Phi \left( p \right) \Leftrightarrow F\left( x \right)$$ $$\Phi \left( w \right) = {1 \over {2\pi …
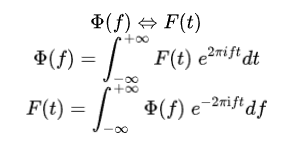

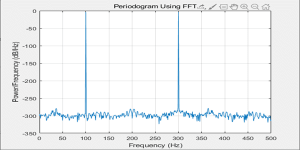
 ) 后仔思考发现,主要是因为功率谱使用了 分贝 为计量单位,比如通过公式 10*log10(Pxx) 将原本的功率谱Pxx进行转换,可见当Pxx处于0~1之间的时候,通过log10(Pxx)转换出来的公式就是负数了。 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号
) 后仔思考发现,主要是因为功率谱使用了 分贝 为计量单位,比如通过公式 10*log10(Pxx) 将原本的功率谱Pxx进行转换,可见当Pxx处于0~1之间的时候,通过log10(Pxx)转换出来的公式就是负数了。 微信公众号 ( Wechat Subscription) 欢迎关注 “结构之旅” 微信公众号