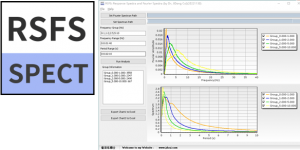
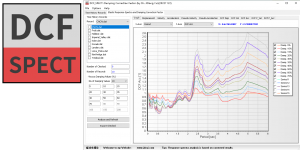
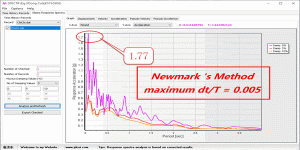
Dynamics [动力学] / Earthquake Engineering [地震工程] / Ground Motion Selection [选波] / My Software [我的软件] / Programming [编程] / Research [科研] / Seismic Design [抗震设计]

[地震动][研究][软件] RSFS: Response Spectra and Fourier Spectra [反应谱及傅里叶谱对比分析工具]

实干、实践、积累、思考、创新。 程序图标( Icon ) 程序介绍 ( Introduction) 随后更新…… 最近做研究写的程序，有需要的人可以关注一下。       相关内容（Related Topics） [01]. [Tool] SPECTR – A program for Response Spectra Analysis [反应谱计算程序] [02]. [程序][Tool] Ground Motion Selection [强震记录选取] [03]. [程序][软件]Ground Motion …

Civil Engineering Test [土木工程试验] / Dynamics [动力学] / Earthquake Engineering [地震工程] / Earthquake isolation and reduction [隔震减震] / My Software [我的软件] / Performance Based Seismic Design [抗震性能设计] / Programming [编程] / Research [科研] / Structural Analysis [结构分析] / Structural Engineering [结构工程]

[地震动][软件][研究] DCF_SPECT: A Tool for Calculating Damping Correction Factor of Earthquake Spectrum [地震反应谱阻尼修正系数计算工具]

实干、实践、积累、思考、创新。 程序图标( Icon ) 程序介绍 ( Introduction) 程序最主要的功能是，计算不同类型反应谱的 阻尼修正系数( Damping Correction Factor )。 程序支持一共支持同时指定 15个阻尼比。 程序支持的反应谱类型包括：相对位移反应谱、相对速度反应谱、绝对加速度反应谱、伪速度反应谱 和 伪加速度反应谱。 程序支持多组地震波动 批量计算 及结果批量输出。 除此之外，程序还有以下特点： （1）多种加速度时程格式支持，一次可导入多组加速度时程 （2）基线修正：软件提供线性和抛物线基线修正方法 对加速度时程进行修正 （3）加速度积分：加速度积分生成相应的位移时程序和速度时程 （4）目前支持以下几种弹性反应谱的分析：相对位移反应谱、相对速度反应谱、绝对加速度反应谱、拟速度反应谱和拟加速度反应谱 （5）支持图形式和表格形式查看时程数据、反应谱数据。表格数据支持复制操作，可方便通过快捷键将数据粘贴至Excel快速绘图 （6）可自由选择坐标轴进行谱曲线绘制，方便谱曲线结果的对比 （7）批量计算分析：加速度时程的积分和反应谱批量分析，并支持批量导出分析结果。 教程及案例 (Examples) …

Earthquake Engineering [地震工程] / My Software [我的软件] / Structural Analysis [结构分析] / Structural Design [结构设计] / Structural Engineering [结构工程]

[动力学][地震动] SPECTR与SeismoSignal反应谱计算有差异？

实干、实践、积累、思考、创新！ 小伙伴用SPECTR （  [软件][工具] SPECTR (v1.0) – A program for Response Spectra Analysis [SPECTR地震波反应谱计算程序]  ）及SeismoSignal做了个反应谱分析对比，发现结果有差异。 如下，对自带的chichi.data地震波进行加速度谱分析。发现差异主要是在0%阻尼比的加速度反应谱上，SPECTR算出来最大是1.77，而seismosignal是1.96，比SPECTR大。 仔细检查原因，发现引起这个差别的主要原因是，SPECTR默认采用的是逐步精确解析法（Piecewise Exact Method）（Nigam-jennings法），该方法不受积步长影响，是更加准确的，而seismosignal 默认采用的是newmark beta法，也只有newmark beta法。 seismosignal 默认采用的是newmark beta： 于是将SPECTR中的积分方法改为newmark beta法，同时参数取值与seismosignal保持一致，然后再重新计算。结果显示，此时SPECTR中的计算结果最大值也是1.96，与seismosignal一致。 因此可以断定这个问题是因为Newmark beta法的积分步长引起的，因为Newmark beta法的计算精度与积分步长有关，尤其是对于阻尼比较小，加速度响应较为敏感。在SPECTR中将Newmark …

Dynamics [动力学] / Earthquake Engineering [地震工程] / Performance Based Seismic Design [抗震性能设计] / Structural Analysis [结构分析] / Structural Design [结构设计] / Structural Engineering [结构工程]

[Dynamics][动力学][抗震] 等效地震力与伪加速度反应谱 (Equivalent Static Lateral Seismic Force and Pseudo-Acceleration Spectrum)

实干、实践、积累、思考、创新。 《建筑抗震设计规范》（GB50011-2010）中给出了采用振型分解反应谱法计算地震作用时的地震力计算公式：\({F_{ji}} = {\alpha _j}{\gamma _j}{X_{ji}}{G_i}\)，其中\({\gamma _j} = \frac{{\sum\limits_{i = 1}^n {{X_{ji}}{G_i}} }}{{\sum\limits_{i = 1}^n {X_{ji}^2{G_i}} }}\)，\({F_{ji}}\)为j振型i质点的水平地震作用标准值；\({\alpha _j}\)为相应于j振型自振周期的地震影响系数；\({X_{ji}}\)为j振型i质点的水平相对位移；\({\gamma _j}\)为振型的参与系数。以下根据结构动力学的相关理论，给出上述公式的一种推导。 1多自由度体系振型分解法 Mode Superposition Method 对于多质点体系，地震动力方程为： $${\left[ M \right]\left\{ {\ddot u} \right\} …