前两天在网上无意看到了很多关于分形的东西。感觉十分漂亮。分形体现了一种有序和无序的统一。有兴趣的可以上网搜些资料看看，还有很多专门的分形软件、网站、论坛。
最出名的分形我想就是MandelbrotSet和JuliaSet了。因为分形几何学的创始人就是IBM研究室的数学家B.B.Mandelbrot。下面简单介绍一下MandelbrotSet和JuliaSet的算法。其实算法原理还是比较简单。
MandelbrotSet由一个二次迭代方程：zn+1 = zn2 +c，z0=c所得到。也就是对所有的复平面上的点c都进行迭代，不发散的点都属于Mandelbrot集的范围。
JuliaSet由一个二次映射：zn+1 = zn2 +c 产生。c为一定值。也就是选定一个常复数，然后对所有的复平面上的点z进行迭代，不发散的点都属于Julia集的范围。
其中z和c都是复数。迭代的次数越多，图形显示就越精细，可以无限细分，同时分形还有自相似性，就是无限放大一个细小的部分，看起来和原来的部分一样。
由于分形的无限性，对图形的显示和算法都是极大的挑战。一般编程的书都会用这个例子来介绍多核计算、并行计算。哈哈。手痒了，还是编个程序来看一下效果吧。截图如下：
1、先是Mandelbrot Set（迭代次数50）：
（1）来个黑白调色方案（黑色的就是Mandelbrot集的范围）
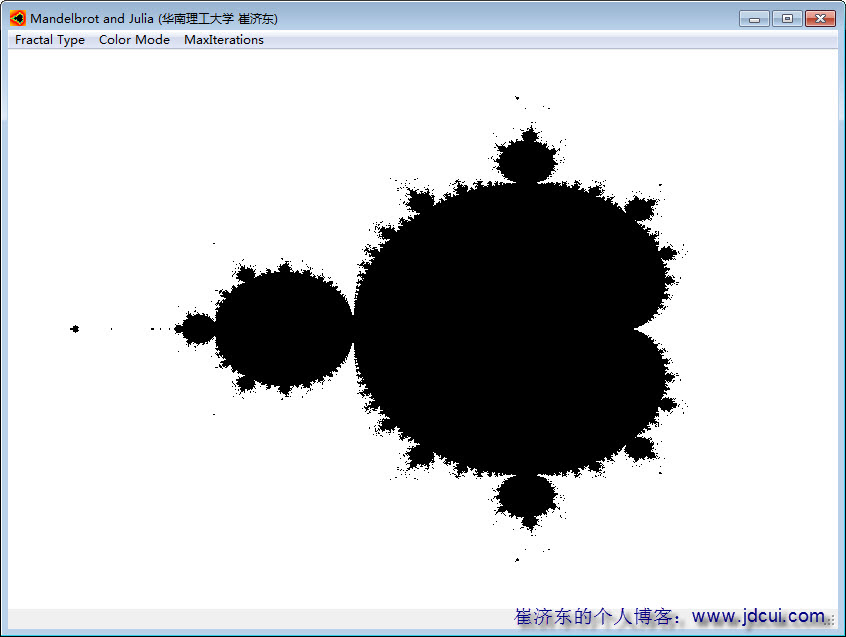
（2）黑白的调色方案太单调了，来看看彩色的效果如何
2、JuliaSet是什么样的呢，我们接下来看看，这次选择迭代次为500次，从下面的图也可以看到，显示的内容更加细致和漂亮。由于Julia集和选择的复常数C有关，下面选择了几个典型的例子来看看效果。
。
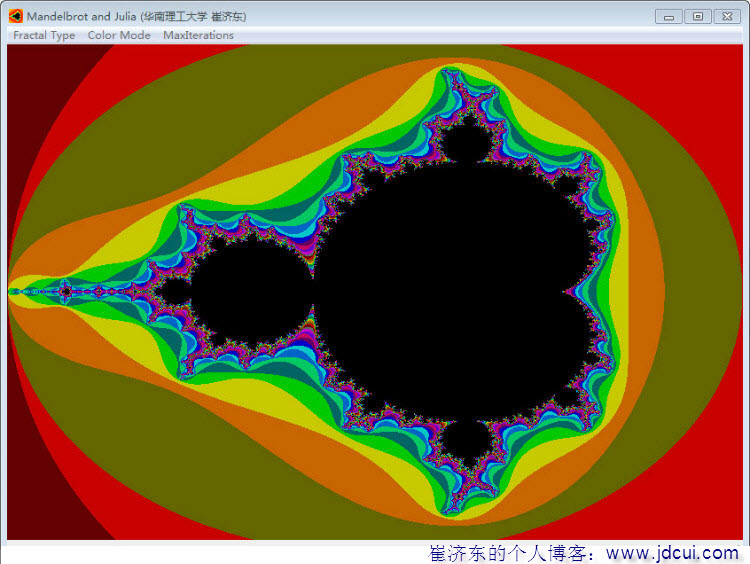
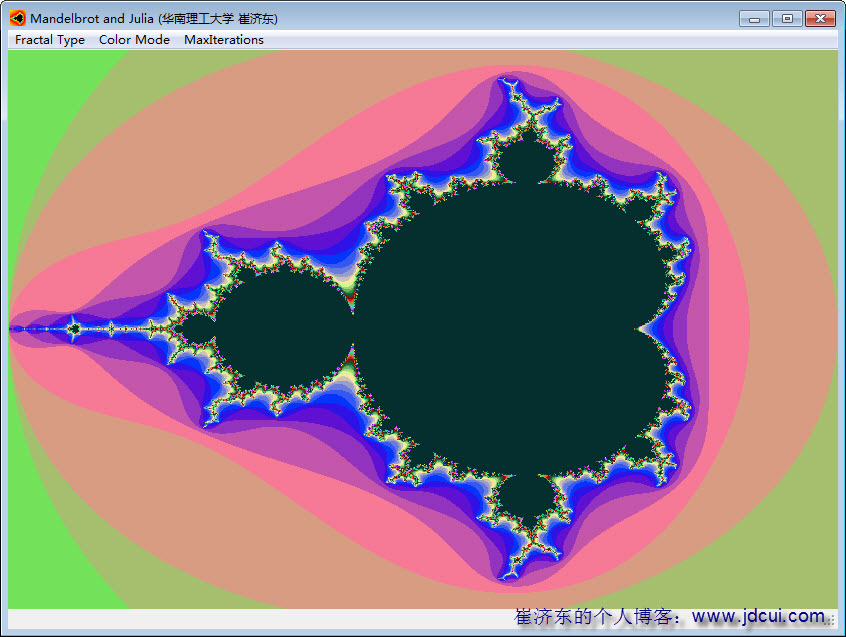
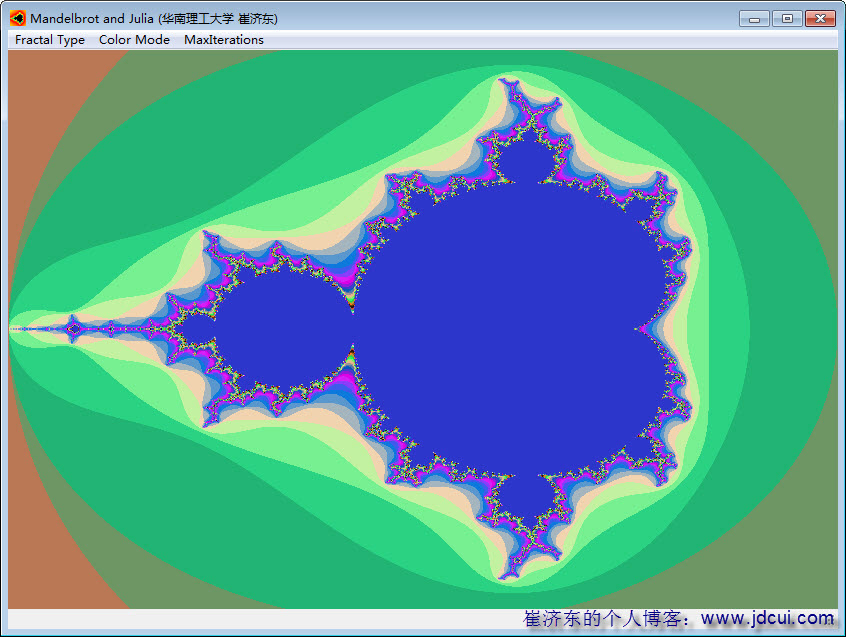
。（1）c=-0.8+0.17i
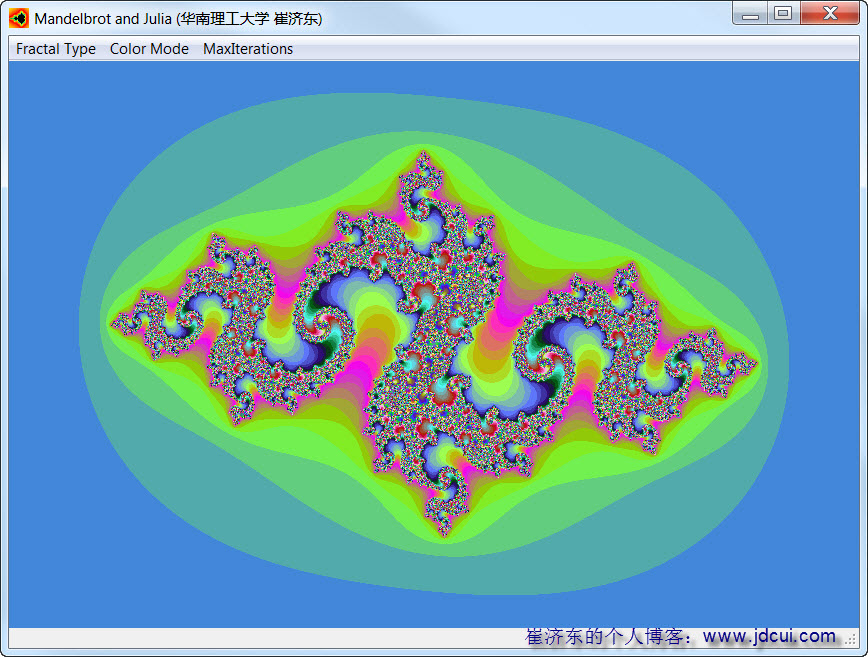
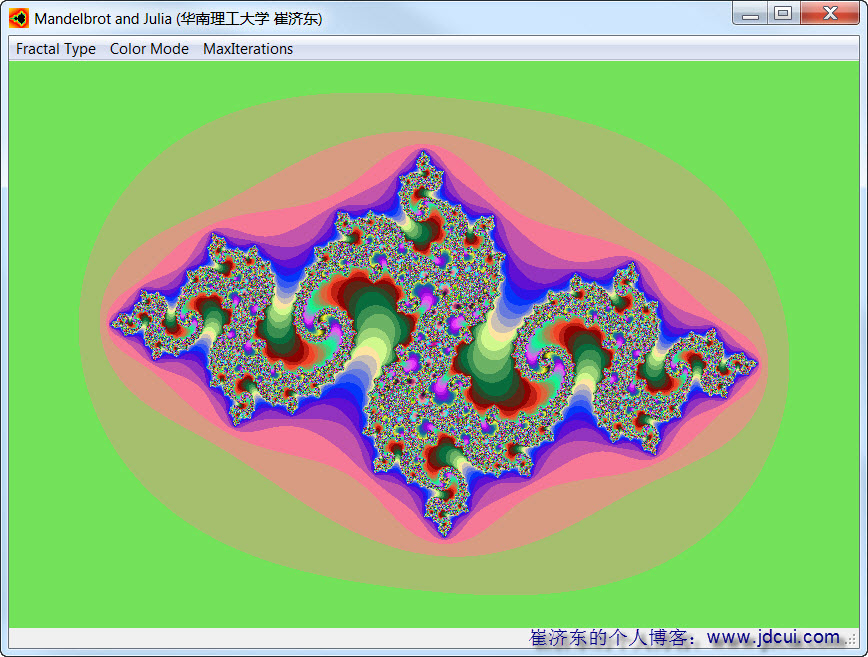
（2）c=-0.7-0.38i
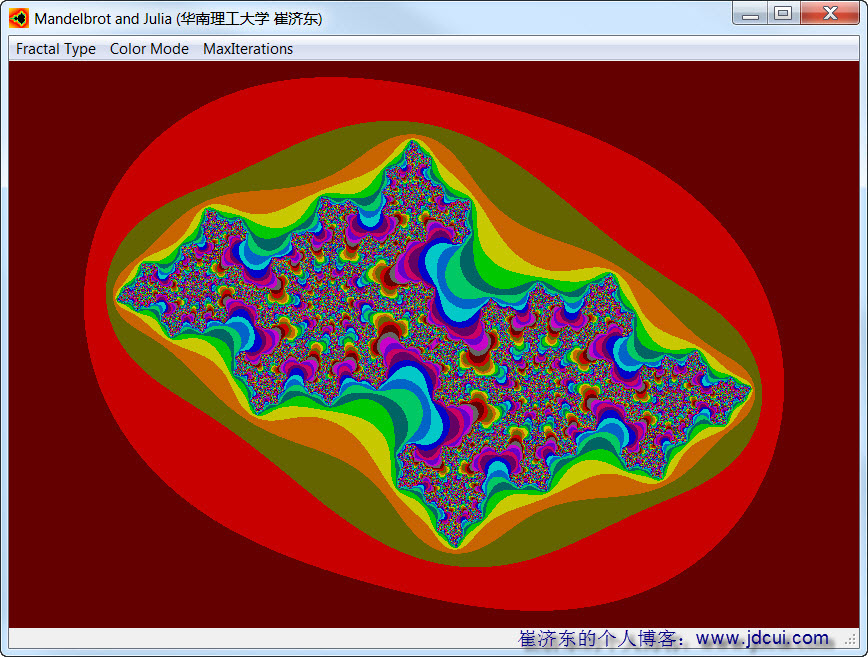
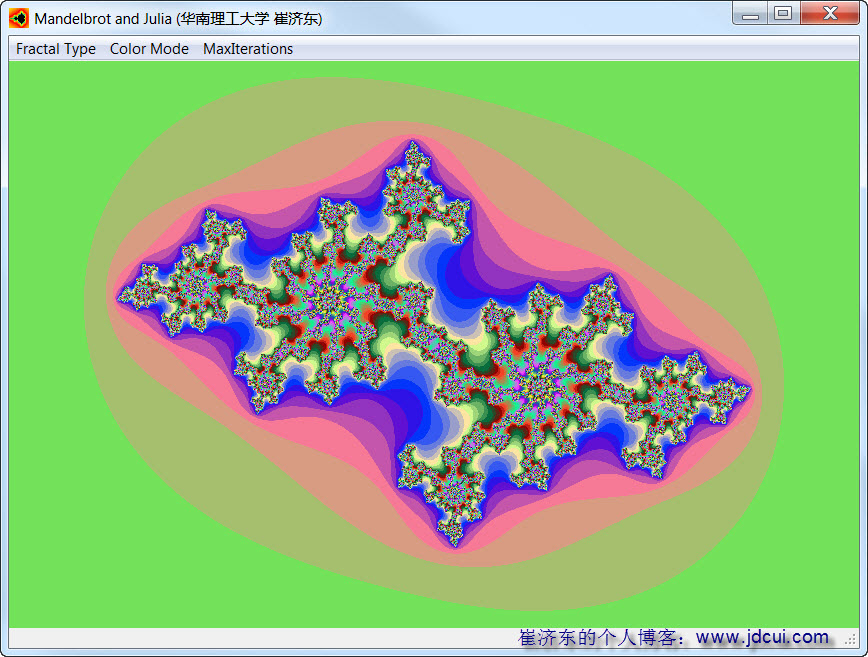
(3) c=0.3
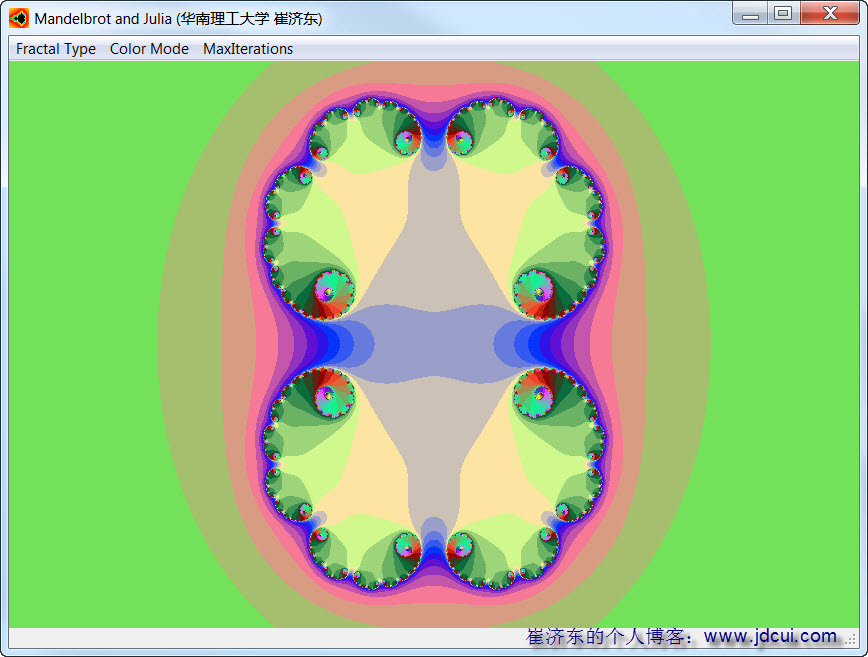
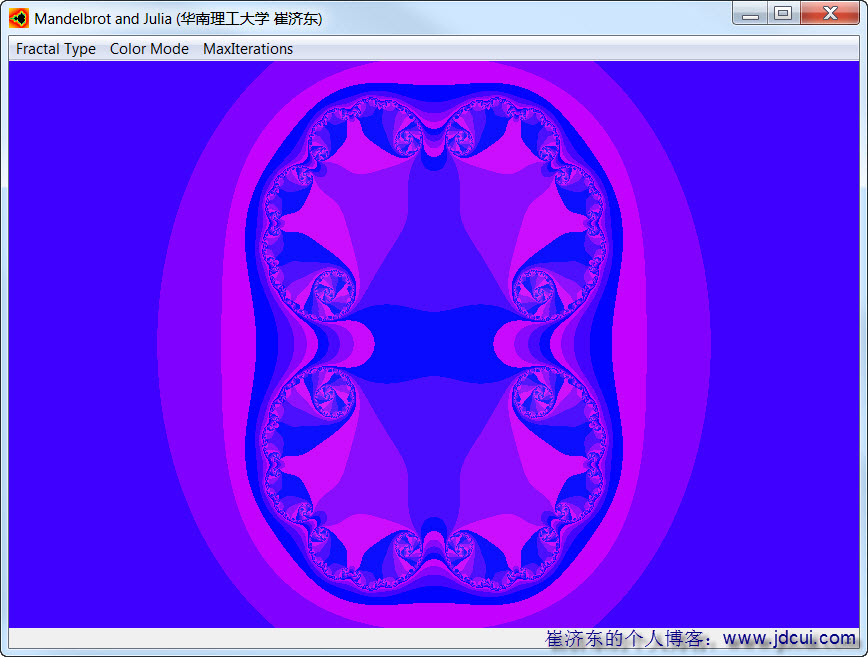
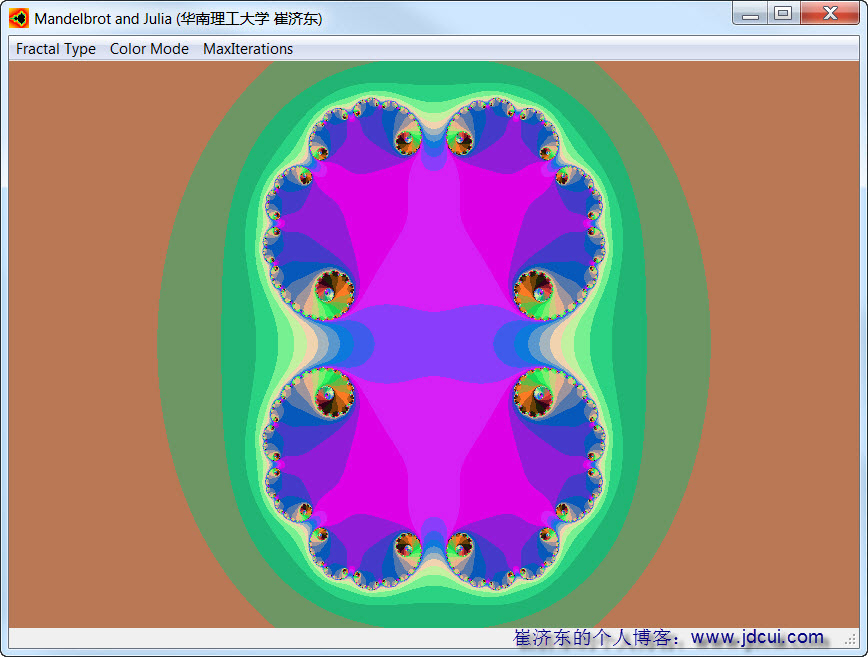
哈哈，真的很漂亮，配色很重要，配色没配好，在网上随便找了几个配色方案。算法也没有仔细去考虑。很多书有专门的分形算法介绍。
小结：数学真的很美，很好玩。
