Structural Analysis [结构分析] / Structural Engineering [结构工程] / Vibration Control [振动控制]

[振动控制] 拍振现象 (Beats Phenomenon)

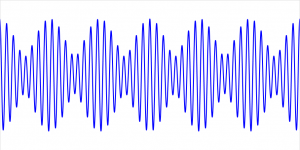
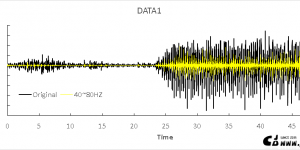
实干、实践、积累、思考、创新。 拍振现象指的是两个频率接近的力（激励源）产生的振动叠加在一起，由于频率接近，周期也接近，每过一个周期两个信号的相对相位就会有一点变化，接近同相的时候两个信号叠加，幅值变大；接近反相的时候两个信号相互抵消，幅值变小，造成波形总幅值的周期性波动。 这里有一些不错的介绍资料，一并列出： [1] Beats：https://www.physicsbootcamp.org/beat-phenomenon.html [2] 航天器火箭发射拍振现象 假定两组波，圆频率分别为ψ1和ψ2的两组波，表达式如下： $${\psi _1}(0,t) = Acos({\omega _1}t) = Acos(2\pi {f_1}t)$$ $${\psi _2}(0,t) = Acos({\omega _2}t) = Acos(2\pi {f_2}t)$$ 叠加后的波表达式如下 $$\psi = {\psi _1} + …

My Software [我的软件] / Structural Engineering [结构工程] / Vibration Control [振动控制]

[软件][振动控制] FOUR_TRAN 案例7: 钢楼梯实测振动数据(不同频率成分对加速度峰值的贡献) (FOUR_TRAN Ex7: Frequency spectrum of measured vibration data of Steel stairs)

实干、实践、积累、思考、创新。 最近参与的一个钢楼梯振动舒适度控制的项目，实测了钢楼梯在不同加载工况下的加速度时程。 在处理数据的时候发现，有些实测曲线整体看来变化较为平稳，有些曲线则会在局部出现一些零散的突兀点，而最大值往往就是这些突兀点控制。 下面是两组这样的曲线，第一组是相对平稳的曲线，第二组是存在明显零散的突兀点。 Data1 Data2 第一直觉，这些突兀点应该是高频成分导致。我们可以采用( [数学][地震动][软件] FOUR_TRAN: Fourier Analysis Tool [傅里叶分析工具] )对其他进行频谱分析，并通过滤波处理，获得不同频率成分的加速度时程，进行对比。 把数据导入FOUR_TRAN，进行分析如下。 第一组曲线不同频率成分的加速度时程曲线 第二组曲线不同频率成分的加速度时程曲线 汇总不同频率成分加速度曲线峰值 由以上分析可见： （1）第二组数据的高频成分比第一组数据大，40HZ~80HZ成分占据了加速度峰值达到原始数据的79.3%，远大于第一组数据的43.1%。 （2）对于第二组数据，零散的突兀点是高频成分所致！高频成分对加速度峰值贡献极大！！ （3） 如果以峰值作为一个评价指标，这个时候高频成分的来源分析就特别重要。如果高频成分是真实的，比如一些附属结构引起，那就必须以实测值为准。如果高频成分是仪器不稳定引起，或者是测试时候受一些异常操作影响，那就应该过滤掉再进行评估。 （4）最后的最后，舒适度需要以真实体感结合为主，数字只是数字。 案例 ( Examples ) [00] [数学][地震动][软件] …