[数学][软件] FOUR_TRAN Example 1: Filtering [FOUR_TRAN傅里叶分析工具使用案例1: 滤波]
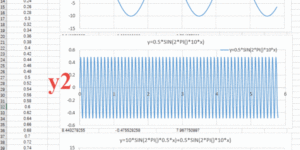
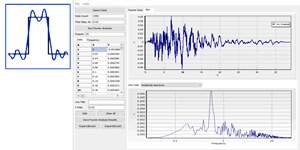
实干、实践、积累、思考、创新。 滤波,傅里叶分析的一个应用。用前面自己写的 FOUR_TRAN 傅里叶分析工具进行分析。 函数 y1: y1=10*SIN(2*PI()*0.5*x),振幅为10,频率为0.5; 函数2: y2=0.5*SIN(2*PI()*10*x),振幅为0.5,频率为10; 函数yw 为函数y1与函数y2的叠加: y=y1+y2 从图可见,由于y2振幅小,频率大,y1振幅大,频率小。叠加后y整体趋势与y1类似,相当于在y1的基础上加上了一些波动。 我么记下来通过傅里叶变化,想办法把从y中把这些波动的y2过滤掉。 打开FOUR_TRAN,导入离散后的函数y,并进行傅里叶分析。 从上图可见,傅里叶变换,可准确解析出两个主要频率成分,一个是0.5,一个时10,其中频率为0.5的傅里叶振幅谱大,而频率为10的傅里叶振幅谱小,能量成分低。与我们前面的函数一致。 接着我们把频率为0.5附近的成分累加起来(逆变换),如下图红色部分,红色曲线基本就是最初的y1,y2被成功过滤掉了。 如下,红儿曲线即是过滤掉频率10后的曲线,曲线与y1一致。 接着我们把频率为10附近的成分累加起来(逆变换),得到下图的红色部分,此时红色部分基本是函数y2,y1成功过滤掉了。 这就是简单的滤波的例子。 关于软件( About the Program) [01] [数学][地震动][软件] FOUR_TRAN: Fourier Analysis …